题目内容
点p是反比例函数y=
上的一点，PD⊥x轴于点D，则△POD的面积为2，则k=________．
-4
分析：根据反比例函数y=（k≠0）系数k的几何意义得到
|k|=2，解得k=±4，然后根据反比例函数的性质确定满足条件的k的值．
解答：∵△POD的面积为2，
∴|k|=2，解得k=±4，
∵反比例函数图象在第二、四象限，
∴k＜0，
∴k=-4．
故答案为-4．
点评：本题考查了反比例函数y=（k≠0）系数k的几何意义：从反比例函数y=（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．
分析：根据反比例函数y=
（k≠0）系数k的几何意义得到|k|=2，解得k=±4，然后根据反比例函数的性质确定满足条件的k的值．解答：∵△POD的面积为2，
∴
|k|=2，解得k=±4，∵反比例函数图象在第二、四象限，
∴k＜0，
∴k=-4．
故答案为-4．
点评：本题考查了反比例函数y=
（k≠0）系数k的几何意义：从反比例函数y=（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|． 
练习册系列答案
相关题目
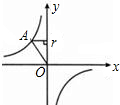如图，点A是反比例函数图象上的一点，自点A向y轴作垂线，垂足为T，已知S△AOT=4，则此函数的表达式为
（2012•东莞模拟）如图，点A是反比例函数
如图所示，在直角坐标系中，点A是反比例函数
如图，点M是反比例函数y=
如图，点P是反比例函数图象上的一点，过点P分别向x轴、y轴作垂线得其阴影部分的面积为8，则该反比例函数的解析式为