题目内容
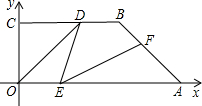
 如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
证明:连结OD,如图,
∵OA为⊙C的直径,
∴∠ADO=90°,
∴OD⊥AB,
∴AD=BD.
分析:连结OD,根据半圆(或直径)所对的圆周角是直角得到∠ADO=90°,然后根据垂径定理即可得到结论.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.

∵OA为⊙C的直径,
∴∠ADO=90°,
∴OD⊥AB,
∴AD=BD.
分析:连结OD,根据半圆(或直径)所对的圆周角是直角得到∠ADO=90°,然后根据垂径定理即可得到结论.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.

练习册系列答案
相关题目

 上的点E处.
上的点E处. 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
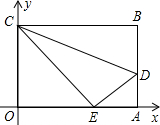
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD= 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.