题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BF平分∠ABC,过点C作CF⊥BF于F点,过A作AD⊥BF于D点.AC与BF交于E点,下列四个结论:①BE=2CF;②AD=DF;③AD+DE=![]() BE;④AB+BC=2AE.其中正确结论的序号是( )
BE;④AB+BC=2AE.其中正确结论的序号是( )

A.只有①②③B.只有②③C.只有①②④D.只有①④
【答案】A
【解析】
适当做辅助线,构建三角形.延长CF并交BA延长线于H
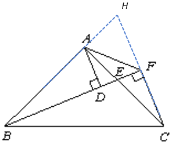
①证明△ABE≌△ACH,得到BE=CH,又可证CH=2CF,故可得BE=2CF
②若要得到AD=DF,则需要证明△ADF为等腰直角三角形,需要证明∠DAF为45°即可
③过E作![]() 交AF于点M,证明△EMF为等腰直角三角形,
交AF于点M,证明△EMF为等腰直角三角形,![]()
![]()
④过E作![]() 于点N,证明
于点N,证明![]() ,得到
,得到![]() ,即可证明④错误.
,即可证明④错误.
①延长BA、CF,交于点H,

∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
![]()
![]()
∴![]()
∵![]()
![]()
∴![]()
∴![]()
②由①知,F为CH中点,又![]() 为直角三角形
为直角三角形
故![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
又BF为![]() 的平分线
的平分线
∴![]()
∴![]()
∴![]()
![]()
在![]() 中,
中,![]()
∴![]()
③过E作![]() 交AF于点M,由②知,CA为∠DAF的平分线
交AF于点M,由②知,CA为∠DAF的平分线
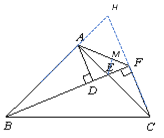
∴![]()
△EMF为等腰直角三角形
∴![]()
∴![]()
④过E作![]() 于点N,可知
于点N,可知![]()
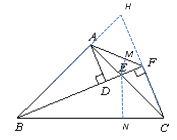
在![]() 中,
中,![]()
∴![]()
即![]() ,而
,而![]()
∴![]()
故![]()
∴![]() ,故④错误,本题答案选A.
,故④错误,本题答案选A.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目




