题目内容
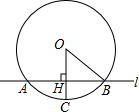 如图,直线l与半径为10cm的⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16厘米,若将直线l通过平移使直线l与⊙O相切,那么直线l平移的距离为( )
如图,直线l与半径为10cm的⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16厘米,若将直线l通过平移使直线l与⊙O相切,那么直线l平移的距离为( )分析:根据垂径定理得到BH=
AB=
×16=8,再利用勾股定理计算出OH,然后利用切线和平移的性质分类讨论:当向下平移时,直线l平移的距离为半径减去OH;当向上平移时,直线l平移的距离为半径加上OH.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AB⊥OC,
∴AH=BH,
∴BH=
AB=
×16=8,
在Rt△BOH中,OB=10,
∴OH=
=
=6,
又∵将直线l通过平移使直线l与⊙O相切,
∴直线l垂直过C点的直径,垂足为直径的两端点,
∴当向下平移时,直线l平移的距离=10-6=4(cm);
当向上平移时,直线l平移的距离=10+6=16(cm).
故选D.
∴AH=BH,
∴BH=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BOH中,OB=10,
∴OH=
| OB2-BH2 |
| 102-82 |
又∵将直线l通过平移使直线l与⊙O相切,
∴直线l垂直过C点的直径,垂足为直径的两端点,
∴当向下平移时,直线l平移的距离=10-6=4(cm);
当向上平移时,直线l平移的距离=10+6=16(cm).
故选D.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了平移的性质、切线的性质以及勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
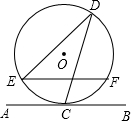 如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为 如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D是圆周上一点,∠ADB=30°.
如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D是圆周上一点,∠ADB=30°.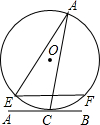 如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( )
如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( ) 如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为