题目内容
 如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为5的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为5
| 3 |
5
.| 3 |
分析:连接OC,OE,由AB为圆的切线,根据切线的性质得到OC与AB垂直,又EF与AB平行,可得出OM垂直于EF,根据垂径定理得到M为EF的中点,可得出EF=2EM,同时由同弧所对的圆心角等于所对圆周角的2倍,根据∠EDC的度数求CHU∠EOM的为60°,在直角三角形OEM中,由半径OE的长,利用锐角三角函数定义及特殊角的三角函数值求出EM的长,进而确定出EF的长.
解答:解:连接OC,OE,如图所示:

∵AB为圆O的切线,
∴OC⊥AB,
∴∠OCB=90°,
又∵EF∥AB,
∴∠OMF=90°,
∴OM⊥EF,
∴EM=FM=
EF,
又∵∠EDC=30°,
∴∠EOM=60°,
在Rt△OEM中,OE=5,∠EOM=60°,
∴sin60°=
,即EM=OEsin60°=
,
则EF=2EM=5
.
故答案为:5

∵AB为圆O的切线,
∴OC⊥AB,
∴∠OCB=90°,
又∵EF∥AB,
∴∠OMF=90°,
∴OM⊥EF,
∴EM=FM=
| 1 |
| 2 |
又∵∠EDC=30°,
∴∠EOM=60°,
在Rt△OEM中,OE=5,∠EOM=60°,
∴sin60°=
| EM |
| OE |
5
| ||
| 2 |
则EF=2EM=5
| 3 |
故答案为:5
| 3 |
点评:此题考查了切线的性质,平行线的性质,垂径定理,锐角三角函数定义,圆周角定理,以及特殊角的三角函数值,遇到直线与圆相切,连接圆心与切点,根据切线的性质得垂直,利用垂径定理及勾股定理来解决问题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
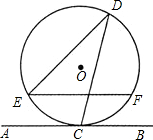 如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为( )
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为( )| A、2 | ||
B、2
| ||
C、
| ||
D、2
|
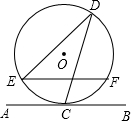 如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为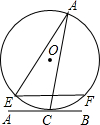 如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( )
如图,直线AB与半径为1的⊙O相切于点C,D是⊙O上一点,且∠EDC=22.5°,弦EF∥AB,则EF的长度为( )