题目内容
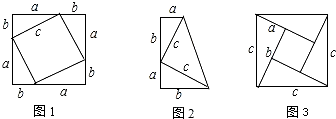
14.2000多年来,人们对直角三角形三边之间的关系的探究颇感兴趣,古往今来,下至平民百姓,上至帝王总统都愿意探究它,研究它的证明,新的证法不断出现.下面给出几种探究方法(由若干个全等的直角三角形拼成如图图形),试用面积法选择其中一种推导直角三角形的三边a、b、c之间的数量关系(1)三边a、b、c之间的数量关系为a2+b2=c2;
(2)理由:(a+b)2=4×$\frac{1}{2}$ab+c2.
分析 (1)由勾股定理即可得出结果;
(2)由大正方形的面积=4个直角三角形的面积+小正方形的面积,即可得出结果.
解答 解:(1)由勾股定理得:a2+b2=c2.故答案为:a2+b2=c2.
(2)选择图1.
∵大正方形的面积=4个直角三角形的面积+小正方形的面积,
∴(a+b)2=4×$\frac{1}{2}$ab+c2,即a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
故答案为:(a+b)2=4×$\frac{1}{2}$ab+c2.
点评 本题考查了勾股定理的证明、正方形和三角形面积的计算方法;熟练掌握勾股定理的证明,通过图形面积关系得出结论是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.如图图案都是同样大小的小正方形按一定的规律组成的,其中第1个图形中有5个小正方形,第2个图形有13个小正方形,第3个图形有25个小正方形,…,按此规律,则第8个图形中小正方形的个数为( )
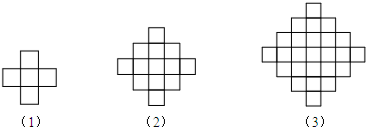
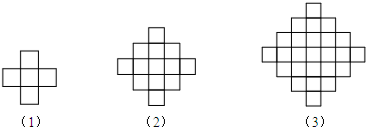
| A. | 181 | B. | 145 | C. | 100 | D. | 88 |
19.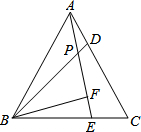 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )| A. | 2 | B. | 3 | C. | 1 | D. | 2$\sqrt{3}$ |
6. 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.
 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.| A. | 9 | B. | 8 | C. | 5 | D. | 4 |