题目内容
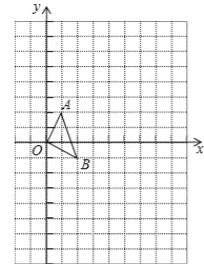
【题目】如图,正方形ABCD的边长为2,P为对角线BD上一动点,以P为直角顶点作Rt△PMN交直线CD于点N,交直线BC于点M,
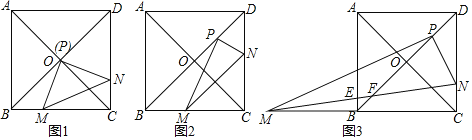
(1)如图1,若点P与对角线交点O重合时,求证:PM=PN.
(2)如图2,若点P为线段OD中点时,
①求证:BM+3DN=3;
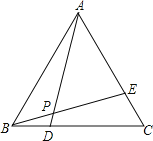
②如图3,当M点在线段CB延长线上,且点N使得3CN=DN,MN分别交AB,BD于E,F,求线段EF的长(直接写出答案).
【答案】(1)见解析;(2)①见解析;② ![]() .
.
【解析】
(1)根据∠MPC=∠NPD,CP=DP,∠PCM=∠PDN=45°,判定△PCM≌△PDN,根据全等三角形的对应边相等,即可得出PM=PN;
(2)如图2,过P作PQ⊥BD,交CD于Q,则∠BPQ=90°,由△MPB∽△NPQ,可得![]() =3,BM=3NQ,由PQ∥OC,点P为线段OD的中点,推出点Q为CD的中点,推出CQ=
=3,BM=3NQ,由PQ∥OC,点P为线段OD的中点,推出点Q为CD的中点,推出CQ=![]() BC=1,推出DN+NQ=1,可得DN+
BC=1,推出DN+NQ=1,可得DN+![]() BM=1,由此即可解决问题.
BM=1,由此即可解决问题.
(3)过P作PQ⊥BD,交CD于Q,判定△PBM∽△PQN,得到![]() ,根据BM=3NQ,求得CN,BM,ME以及EN的长,再根据△MBE∽△MCN,△BEF∽△DNF,即可得出EN的长,根据相似三角形的性质得到线段EF的长.
,根据BM=3NQ,求得CN,BM,ME以及EN的长,再根据△MBE∽△MCN,△BEF∽△DNF,即可得出EN的长,根据相似三角形的性质得到线段EF的长.
解:(1)如图1中,
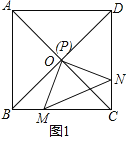
依题意得,∠MPN=∠CPD=90°,
∴∠MPC=∠NPD,
又∵正方形ABCD中,AC、BD交于点O,
∴CP=DP,∠PCM=∠PDN=45°,
在△PCM和△PDN中,
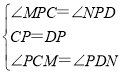 ,
,
∴△PCM≌△PDN(ASA),
∴PM=PN;
(2)①证明:如图2,过P作PQ⊥BD,交CD于Q,则∠BPQ=90°,
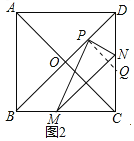
∴∠PQD=∠PBM=45°,
依题意得,∠MPN=∠QPD=90°,
∴∠MPB=∠NPQ,
∴△MPB∽△NPQ,
∴![]() ,
,
∵点P为线段OD的中点,OB=OD,
∴BP=3PD,
∵PD=PQ,
∴PB=3PQ,
∴![]() ,即BM=3NQ,
,即BM=3NQ,
∵PQ∥OC,点P为线段OD的中点,
∴点Q为CD的中点,
∴CQ=![]() BC=1,
BC=1,
∴DN+NQ=1,
∴DN+![]() BM=1,
BM=1,
∴BM+3DN=3.
②如图3,过P作PQ⊥BD,交CD于Q,则∠BPQ=∠MPN=90°,∠PQD=45°,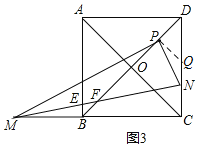
∴∠MPB=∠NPQ,
∵∠PQD=∠PBC=45°,
∴∠PBM=∠PQN=135°,
∴△PBM∽△PQN,
∴![]() ,
,
又∵点P为线段OD的中点,
∴PD=![]() PB=PQ,
PB=PQ,
∴![]() ,即BM=3NQ,
,即BM=3NQ,
∵CN=![]() DN=
DN=![]() CD=
CD=![]() ,
,
∴DN=![]() ,
,
∵PQ∥OC,P为线段OD的中点,
∴Q为CD的中点,
∴DQ=CQ=CD=1,
∴NQ=1-![]() =
=![]() ,
,
∴BM=3NQ=,CM=![]() +2=
+2=![]() ,
,
∴Rt△CMN中,MN=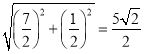 ,
,
∵EB∥NC,
∴△MBE∽△MCN,△BEF∽△DNF,
∴![]() ,即
,即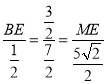 ,
,
∴BE=![]() ,ME=
,ME=![]() ,
,
∴EN=MN-ME=![]() ,
,
∵![]() ,
,
∴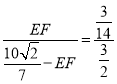 ,
,
解得EF=![]() .
.
故答案为:(1)见解析;(2)①见解析;② ![]() .
.

 优生乐园系列答案
优生乐园系列答案