题目内容
如图所示,∠MBN=45°,若△ABC的顶点A在射线BM上,且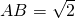 ,点C在射线BN上运动(C不与B重合),请你探究:
,点C在射线BN上运动(C不与B重合),请你探究:
(1)若△ABC是直角三角形,试求线段BC的长,并将点C的位置标注在图形中;

(2)探究:①当BC的值在什么范围时,△ABC是锐角三角形;

②当BC的值在什么范围时,△ABC是钝角三角形.

解:①如图所示,

当∠ACB=90°时,则BC= AB=1;
AB=1;
当∠BAC=90°时,则BC= AB=2.
AB=2.
即BC=1或2时,△ABC是直角三角形;
②当1<BC<2时,△ABC是锐角三角形;
③当BC<1或BC>2时,△ABC是钝角三角形.
分析:①若△ABC是直角三角形,则有两种情况:∠ACB=90°或∠BAC=90°.根据等腰直角三角形的性质进行计算BC的长;
②结合图形,知要使△ABC是锐角三角形,则应介于①的两种情况之间;
③结合图形,知要使△ABC是钝角三角形,则应小于①中求得的较小的BC或大于①中求得的较大的BC的长.
点评:此题综合运用了等腰直角三角形的性质,能够结合图形分析不同形状的三角形的取值范围.

当∠ACB=90°时,则BC=
 AB=1;
AB=1;当∠BAC=90°时,则BC=
 AB=2.
AB=2.即BC=1或2时,△ABC是直角三角形;
②当1<BC<2时,△ABC是锐角三角形;
③当BC<1或BC>2时,△ABC是钝角三角形.
分析:①若△ABC是直角三角形,则有两种情况:∠ACB=90°或∠BAC=90°.根据等腰直角三角形的性质进行计算BC的长;
②结合图形,知要使△ABC是锐角三角形,则应介于①的两种情况之间;
③结合图形,知要使△ABC是钝角三角形,则应小于①中求得的较小的BC或大于①中求得的较大的BC的长.
点评:此题综合运用了等腰直角三角形的性质,能够结合图形分析不同形状的三角形的取值范围.

练习册系列答案
相关题目



 如图所示,∠MBN=45°,若△ABC的顶点A在射线BM上,且AB=
如图所示,∠MBN=45°,若△ABC的顶点A在射线BM上,且AB= (3)当BC的值在 范围时,△ABC是钝角三角形 .
(3)当BC的值在 范围时,△ABC是钝角三角形 .
 ,点C在射线BN运动(C
,点C在射线BN运动(C
 ,点C在射线BN运动(C
,点C在射线BN运动(C