题目内容
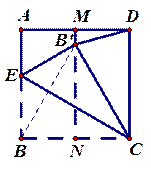
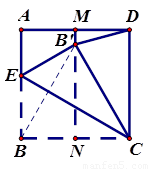
如图，试求∠A+∠B+∠C+∠D+∠E的度数．分析：连 BC，根据三角形的内角和定理即可证得∠E+∠D=∠1+∠2，然后根据三角形的内角和定理即可求解．
解答：
解：连结BC，∵∠E+∠D+∠EFD=∠1+∠2+∠BFC=180°，
又∵∠EFD=∠BFC，
∴∠E+∠D=∠1+∠2，
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠ABD+∠ACE+∠1+∠2
=∠ABC+∠A+∠ACB
=180゜．
解：连结BC，∵∠E+∠D+∠EFD=∠1+∠2+∠BFC=180°，又∵∠EFD=∠BFC，
∴∠E+∠D=∠1+∠2，
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠ABD+∠ACE+∠1+∠2
=∠ABC+∠A+∠ACB
=180゜．
点评：本题考查了三角形的内角和定理，正确作出辅助线，证明∠E+∠D=∠1+∠2是关键．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图，试求阴影部分的面积．（用含a的代数式表示）
