Question

19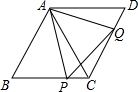．如图，已知菱形ABCD的边长为2，∠B=60°，∠PAQ=60°且∠PAQ绕着点A在菱形ABCD内部旋转，在运动过程中△PCQ的面积最大值是$\frac{1}{4}\sqrt{3}$．

Answer 1

分析 先根据已知条件判定△ACP≌△ADQ，得出△PAQ是等边三角形，再求得四边形APCQ的面积为菱形面积的一半，最后根据三角形APQ的面积最小值，求得三角形PCQ的面积最大值．

解答 解：∵在菱形ABCD中，∠B=60°，
∴△ABC是等边三角形，
∴AB=BC=AC，∠ACP=∠CAD=60°，
∴AC=AD，
∵∠PAQ=60°，
∴∠CAP=∠DAQ，
∴△ACP≌△ADQ，
∴AP=AQ，
∴△PAQ是等边三角形，
∵△ACP≌△ADQ，
∴S_△ACP=S_△ADQ，即S_{四边形APCQ}=S_△ACD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$（定值），
∵当三角形APQ的面积最小时，三角形PCQ的面积最大，
∴当AP⊥BC时，AP=$\sqrt{3}$，三角形APQ的面积最小值=$\frac{\sqrt{3}}{4}×（\sqrt{3}）^{2}$=$\frac{3}{4}\sqrt{3}$，
∴三角形PCQ的面积最大值=$\sqrt{3}$-$\frac{3}{4}\sqrt{3}$=$\frac{1}{4}\sqrt{3}$．
故答案为：$\frac{1}{4}\sqrt{3}$

点评 本题主要考查了菱形和等边三角形，解决问题的关键是确定四边形APCQ的面积为定值，等于菱形面积的一半．当∠PAQ绕着点A在菱形ABCD内部旋转时，三角形APQ的形状不变，但大小发生改变，根据垂线段最短可知其面积存在最小值．