题目内容
18.在平面直角坐标系xOy中,二次函数y=mx2-(m+n)x+n(m<0)的图象与y轴正半轴交于A点,求证:该二次函数的图象与x轴必有两个交点.分析 首先根据题意得出n的符号,进而求出b2-4ac的符号,进而得出答案.
解答 证明:∵二次函数y=mx2-(m+n)x+n(m<0)的图象与y轴正半轴交于A点,
∴n>0,
∴m-n<0,
∴b2-4ac=(m+n)2-4mn=(m-n)2>0,
∴该二次函数的图象与x轴必有两个交点.
点评 此题主要考查了抛物线与x轴交点,正确得出b2-4ac的符号是解题关键.

练习册系列答案
相关题目
9.下列各式中,能用平方差公式计算的是( )
| A. | (3x+2y)(2x-3y) | B. | (2x+3)(3-2x) | C. | (2b-a)(a-2b) | D. | (m+2)(n-2) |
6.已知正比例函数y=(2m-1)x在图象上有两点A(x1、y1)、B(x2、y2),当x1<2时,y1<y2,则m的取值范围是( )
| A. | m$<\frac{1}{2}$ | B. | m$>\frac{1}{2}$ | C. | m<2 | D. | m>0 |
8.小军同学学习完有理数后,写了下列四个式子,其中是负数的是( )
| A. | -(-2) | B. | -|-2| | C. | (-6)2 | D. | $(-\frac{1}{2})^{2014}$ |
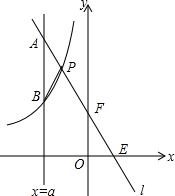 如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.