Question

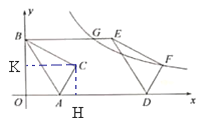
【题目】如图，点A，B分别在x轴、y轴上，点O关于AB的对称点C在第一象限，将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点)，点F落在双曲线y=上，连结BE交该双曲线于点G．∠BAO=60°，OA=2GE，则k的值为 ________ ．

Answer 1

【答案】

【解析】

设OA等于2m， 由对称图形的特点，和勾股定理等把C点和B点坐标用含m的代数式来表示，F、E、G是由△ABC平移K个单位得到，坐标可以用含m和k的代数式表示，因为G、F在双曲线上，所以其横纵坐标的乘积都为k，据此列两个关系式，先求出m的值，从而可求k的值.

如图：作CH垂直于x轴，CK垂直于y轴，

由对称图形的特点知，CA=OA， 设OA=2m，

∵∠BAO=60°，

∴OB=2，AC=2m， ∠CAH=180°-60°-60°=60°，

∴AH=m，CH=，

∴C点坐标为（3m， ），

则F点坐标为（3m+k， ），

F点在双曲线上，则(3m+k)×=k，

B点坐标为（0，2），

则E点坐标为（k，2），

G点坐标为（k-m，2），

则(k-m) × 2m=k，

∴(3m+k)×m=(k-m) ×2m，

整理得k=5m，代入(k-m)2m=k中，

得4m×2m=5m，

即m=0(舍去)，m=，

则，

故答案为：.