题目内容
3.观察下列各等式,并回答问题:$\frac{1}{1×2}$=1-$\frac{1}{2}$; $\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$; $\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$; $\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$;…
(1)填空:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$(n是正整数)
(2)计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2004×2005}$=$\frac{2004}{2005}$.
(3)计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$.
(4)求$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$+…+$\frac{1}{2013×2015}$的值.
分析 (1)根据题意确定出拆项规律,写出第n个式子即可;
(2)根据拆项规律,先拆项再抵消写即可求解;
(3)根据拆项规律,先拆项再抵消写即可求解;
(4)根据拆项规律,先拆项再抵消写即可求解.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$(n是正整数)
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2004×2005}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2004}$-$\frac{1}{2005}$
=1-$\frac{1}{2005}$
=$\frac{2004}{2005}$.
(3)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{n(n+1)}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$.
(4)$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$+…+$\frac{1}{2013×2015}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2013}$-$\frac{1}{2015}$)
=$\frac{1}{2}$×(1-$\frac{1}{2015}$)
=$\frac{1}{2}$×$\frac{2014}{2015}$
=$\frac{1007}{2015}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$; (2)$\frac{2004}{2005}$;(3)$\frac{n}{n+1}$.
点评 考查了有理数的混合运算,(4)的关键是将式子变形为$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2013}$-$\frac{1}{2015}$)进行计算.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{m+1}{n+1}$=$\frac{m}{n}$ | B. | $\frac{(x+a)(x-b)+2b}{(x+a)(x+b)}$=1 | ||
| C. | $\frac{{b}^{2}-{a}^{2}}{a-b}$=-b-a | D. | x$÷y×\frac{2}{y}=\frac{x}{2}$ |
| A. | 条形统计图 | B. | 扇形统计图 | C. | 频数分布图 | D. | 折线统计图 |
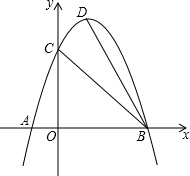 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,交y轴正半轴于C点,D为抛物线的顶点,点P在x轴上,且∠PCB=∠CBD,求点P的坐标.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,交y轴正半轴于C点,D为抛物线的顶点,点P在x轴上,且∠PCB=∠CBD,求点P的坐标.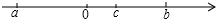 (1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简
(1)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简