Question

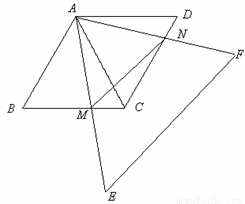
如图，两个同样大小的等边△ABC和△ACD，边长为a，它们拼成一个菱形ABCD，另一个足够大的等边△AEF绕点A旋转，AE与BC相交于点M，AF与CD相交于点N．
（1）证明：∠DAN=∠CAM；
（2）求四边形AMCN的面积；
（3）探索△AMN何时面积最小，并写出这个最小面积的值．

Answer 1

分析：（1）由△ABC和△ACD，△AEF都是等边三角形，得到∠DAC=∠FAE=60°，得到∠DAN=∠CAM；
（2）由（1）和等边三角形的性质得到∠DAN=∠CAM，AD=AC，∠D=∠ACB=60°，则△ADN≌△ACM，于是有S_{四边形AMCN的面积}=S_△ABC=

3

4

a²；
（3）由（2）得AN=AM，再根据三角形的面积公式得S_△AMN=

1

2

AM•AN•sin∠NAM=

1

2

AM²•sin60°=

3

4

×AM²，当AM最小时，S_△AMN最小，即AM为BC边上的高，而AM=

3

2

a，即可得到△AMN面积最小值．

解答：（1）证明：∵△ABC和△ACD，△AEF都是等边三角形，
∴∠DAC=∠FAE=60°，
∴∠DAN=∠CAM；

解：（2）∵∠DAN=∠CAM，AD=AC，∠D=∠ACB=60°，
∴△ADN≌△ACM，
∴S_{四边形AMCN的面积}=S_△ABC=

3

4

a²；

（3）∵△ADN≌△ACM，
∴AN=AM，
∴S_△AMN=

1

2

AM•AN•sin∠NAM=

1

2

AM²•sin60°=

3

4

×AM²，
当AM最小时，S_△AMN最小，即AM为BC边上的高，
∴AM=

3

2

a，
∴△AMN面积最小值=

3

4

×

3

4

×a²=

3 3

16

a²．

点评：本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．也考查了三角形全等的判定与性质和等边三角形的性质以及它的面积公式．