Question

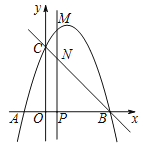
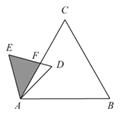
【题目】如图，已知△ABC是面积为的等边三角形，△ABC∽△ADE，AB＝2AD，∠BAD＝45°，AC与DE相交于点F，则△AEF的面积等于 （结果保留根号）．

Answer 1

【答案】．

【解析】

试题∵AB=2AD，

∴=2，

又∵△ABC∽△ADE，△ABC是面积为，

∴=4，

∴S△ADE=，

∵△ABC∽△ADE，△ABC是等边三角形，

∴△ADE也是等边三角形，其面积为AE2=，

∴AE=1，

作FG⊥AE于G，

∵∠BAD=45°，∠BAC=∠EAD=60°，

∴∠EAF=45°，

∴△AFG是等腰直角三角形，

设AG=FG=h，在直角三角形FGE中，

∵∠E=60°，EG=1﹣h，FG=h，

∴tan∠E=，即tan60°=，解得h=，

∴S△AEF=×1×=．