题目内容
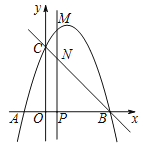
【题目】如图，抛物线
与
轴交于
、
两点（点
在点
的左侧），点
的坐标为
，与
轴交于点
，作直线
．动点
在
轴上运动，过点
作
轴，交抛物线于点
，交直线
于点
，设点
的横坐标为
．
（Ⅰ）求抛物线的解析式和直线
的解析式；
（Ⅱ）当点
在线段
上运动时，求线段
的最大值；
（Ⅲ）当以
、
、
、
为顶点的四边形是平行四边形时，直接写出
的值．
【答案】（1）y=﹣x2+2x+3，y=﹣x+3；（2）当m=
时，MN有最大值，MN的最大值为
；（3）
或
．
【解析】（1）由A、C两点的坐标利用待定系数法可求得抛物线解析式，则可求得B点坐标，再利用待定系数法可求得直线BC的解析式；
（2）用m可分别表示出N、M的坐标，则可表示出MN的长，再利用二次函数的最值可求得MN的最大值；
(3) 由条件可得出MN=OC，结合（2）可得到关于m的方程，可求得m的值
本题解析：
（1）∵抛物线过A、C两点，
∴代入抛物线解析式可得
，解得
，
∴抛物线解析式为y=﹣x2+2x+3，
令y=0可得，﹣x2+2x+3=0，解x1=﹣1，x2=3，
∵B点在A点右侧，
∴B点坐标为（3，0），
设直线BC解析式为y=kx+s，
把B、C坐标代入可得
，解得
，
∴直线BC解析式为y=﹣x+3；
（2）∵PM⊥x轴，点P的横坐标为m，
∴M（m，﹣m2+2m+3），N（m，- m+3），
∵P在线段OB上运动，
∴M点在N点上方，
∴MN=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m=﹣（m﹣
）2+
，
∴当m=
时，MN有最大值，MN的最大值为
；
（3）∵PM⊥x轴，
∴MN∥OC，
当以C、O、M、N为顶点的四边形是平行四边形时，则有OC=MN，
当点P在线段OB上时，则有MN=﹣m2+3m，
∴﹣m2+3m=3，此方程无实数根，
当点P不在线段OB上时，则有MN=﹣m+3﹣（﹣m2+2m+3）=m2﹣3m，
∴m2﹣3m=3，解得m=
或m=
，
综上可知当以C、O、M、N为顶点的四边形是平行四边形时，m的值为
或
．
