Question

（2012•中山区一模）在△ABC中，∠ACB=90°，以AC为一边向外作正方形ACDE（如图1），线段BA绕点A顺时针旋转90°，得线段AP，连接PE、CE．

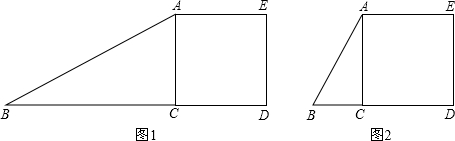
（1）①请补全图形；
②当tan∠BAC=2时，探究线段PE与CE的关系，并加以证明；
（2）当tan∠BAC=n时（如图2），请直接写出PE：CE的值．（用含有n的式子表示）

Answer 1

分析：（1）①根据题意画出图形即可；
②过点P作PF⊥EA的延长线于点F，由全等三角形的判定定理可得出Rt△APF≌Rt△ABC，设AC=x，由tan∠BAC=2，可知BC=2x，在Rt△ACE中，利用勾股定理可求出CE的长，在Rt△PEF中由勾股定理得出PE的长，再求出其比值即可；
（2）同（1）可得Rt△APE≌Rt△ABC，AF=AC，PF=BC，tan∠BAC=n，设AC=x，则BC=nx，同上可得出CE及PE的长，故可得出结论．

解答：（1）解：①如图1所示：
②PE=2CE．
证明：如图2所示，过点P作PF⊥EA的延长线于点F，
∵四边形ACDE是正方形，
∴∠2+∠FAB=90°，
∵线段AP是由线段AB绕点A顺时针旋转90°得到，
∴∠1+∠FAB=90°，AP=AB，
∴∠1=∠2，
∵PF⊥AF，
∴∠ACB=∠PFA=90°，
∴∠APF=∠ABC，
在Rt△APF与Rt△ABC中，
∵

∠1=∠2 AP=AB ∠APF=∠ABC

，
∴Rt△APF≌Rt△ABC，
∴AF=AC，PF=BC，
设AC=x，
∵tan∠BAC=2，
∴BC=2x，
在Rt△ACE中，
CE=

AE2+AC2

=

x2+x2

=

2

x，
在Rt△PEF中，
∵AF=AE=x，PF=BC=2x，
∴EF=2x，
∴PE=

PF2+EF2

=

(2x)2+(2x)2

=2

2

x，
∴

PE

CE

=

2 2 x

2 x

=2，即PE=2CE；

（2）

PE

CE

=

n2+4 x

2 x

=

n2+4

2

．
证明：同（1）可得Rt△APF≌Rt△ABC，AF=AC，PF=BC，
∵tan∠BAC=n，
∴设AC=x，则BC=nx，
在Rt△ACE中，
CE=

AE2+AC2

=

x2+x2

=

2

x，
在Rt△PEF中，
∵AF=AE=x，PF=BC=nx，
∴EF=2x，
∴PE=

PF2+EF2

=

(nx)2+(2x)2

=

n2+4

x，
∴

PE

CE

=

n2+4 x

2 x

=

n2+4

2

．

点评：本题考查的是相似形综合题，涉及到全等三角形的判定与性质及图形旋转的性质，根据题意画出图形，能利用数形结合求解是解答此题的关键．