题目内容
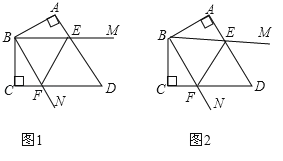
【题目】如图1,在等腰![]() 中,
中,![]() 为中线,将线段
为中线,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ;得到线段
;得到线段![]() 连接
连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
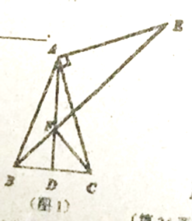
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 是钝角时,
是钝角时,
①请在图2中依题意补全图形,并标出对应字母;
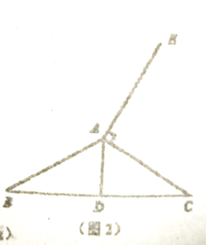
②探究图2中![]() 的形状,并说明理由;
的形状,并说明理由;
③若![]() 则
则![]() .
.
【答案】(1)45°;(2)①见解析;②![]() 是等腰直角三角形,理由见解析;③
是等腰直角三角形,理由见解析;③![]()
【解析】
(1)根据等腰△ABC的性质可得∠BAD的角度,从而得出∠ABD的角度;在等腰△ABE中,可推导得出∠ABE的大小,从而得出∠FBC;
(2)①根据题干要求补全图形即可;
②如下图,根据等腰△FBC的性质可得到△FAB≌△FAC,从而得∠FBA=∠FCA,再根据旋转特点,可得∠FBA=∠AFB,最后利用Rt△AEC和△CEF之间的角度转化可得∠EFC=90°,从而得出三角形形状;
③在Rt△AEC中,可求得EC的长,再在Rt△BFC中求得FC的长,最后在Rt△EFC中得出EF的长.
(1)∵AE是AC绕点A逆时针旋转90°所得
∴∠CAE=90°,CA=AE
∵AB=AC,
∴AB=AE
∵∠BAC=30°,AD是等腰三角形的中线
∴∠BAD=∠DAC=15°,AD⊥BC
∴∠BAE=120°
∴在△ABE中,∠ABE=∠E=30°
在△ADB中,∠ABD=75°
∴∠FBC=45°
(2)①如下图:
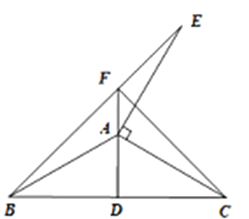
![]() 是等腰直角三角形
是等腰直角三角形
②![]() 是等腰直角三角形,理由如下
是等腰直角三角形,理由如下
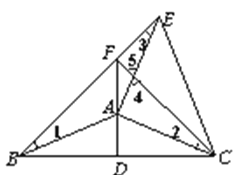
![]()
![]() .
.
![]() 是
是![]() 的垂直平分线
的垂直平分线
![]()
又![]()
![]()
![]()
由旋转可知![]() ,又
,又![]() .
.
![]()
![]()
![]()
又![]()
![]()
即
又![]() .
.
![]() 为等腰直角三角形
为等腰直角三角形
③∵AB=5,
∴AC=5
∵△ACE是等腰直角三角形
∴可得:AE=5,EC=![]()
∵BC=8
∴在等腰直角三角形FBC中,FB=FC=4![]()
∴在Rt△EFC中,EF=![]()

练习册系列答案
相关题目