题目内容
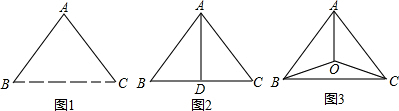
一个边长为4㎝的等边三角形 与⊙
与⊙ 等高,如图放置, ⊙
等高,如图放置, ⊙ 与
与 相切于点
相切于点 ,⊙
,⊙ 与
与 相交于点
相交于点 ,则
,则 的长为 ㎝.
的长为 ㎝.
3
解析考点:切线的性质;垂径定理;圆周角定理;弦切角定理.
分析:连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边高的  倍.题目中一个边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
倍.题目中一个边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为  ,即OC=
,即OC=  ,
,
又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
解:连接OC,并过点O作OF⊥CE于F,
且△ABC为等边三角形,边长为4,
故高为2 ,即OC=
,即OC= ,
,
又∠ACB=60°,故有∠OCF=30°,
在Rt△OFC中,可得FC= ,
,
即CE=3.
故答案为:3.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
若圆锥的轴截面是一个边长为2cm的等边三角形,则这个圆锥的侧面积是( )
| A、2πcm2 | B、2cm2 | C、4πcm2 | D、4cm2 |

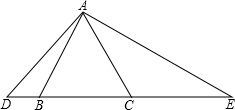 如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°
如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°