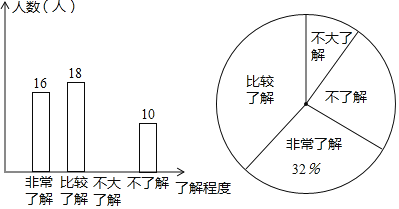
题目内容
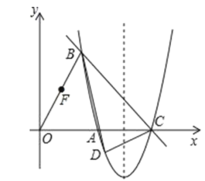
【题目】在平面直角坐标系中，抛物线y=
，经过点A（1，3）、B（0，1），过点A作x轴的平行线交抛物线于另一点C．
（1）求抛物线的表达式及其顶点坐标；
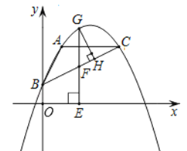
（2）如图，点G是BC上方抛物线上的一个动点，分别过点G作GH⊥BC于点H、作GE⊥x轴于点E，交BC于点F，在点G运动的过程中，△GFH的周长是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．
【答案】（1）y=
，顶点坐标为：
；（2）存在，最大值为：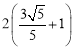
.
【解析】
（1）根据待定系数法求解即可；
（2）先根据题意得出点C的坐标，从而得出直线BC的方程，求出BC的长，再根据△BCI∽△FGH得出
，从而
，G(m, 
)，则F(m, 
)得出
，当m=2时，△GFH的周长有最大值．
（1）∵抛物线y=
过点A（1，3）、B（0，1），
∴
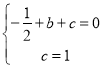，解得：
，
即抛物线的表达式为：y=，
y=
=
，
∴顶点坐标为：；
（2）∵A（1，3），由对称轴可知C（4，3）
由B（0，1）、C（4，3），
得直线BC的解析式为：
，BC=
，
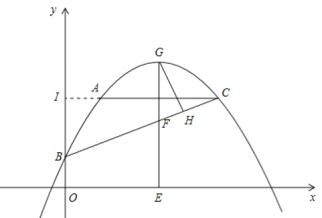
由题意知，∠ACB=∠FGH，
延长CA与y轴交于点I，则I（0，3）
∴BI=2，CI=4，
由△BCI∽△FGH，得：
,
即
，
∴
，
，
即△GFH的周长为：C=FH+GH+FG=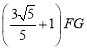
，
设G(m, )，则F(m, )，
∴C=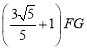
=
=
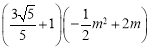
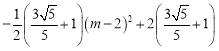
∴当m=2时，△GFH的周长有最大值，最大值为：.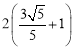
练习册系列答案
阅读快车系列答案
相关题目
