题目内容
已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点E,且E为 的中点.
的中点.
(1)求证:AC是半圆O的切线;
(2)若AD=6,AE=6 ,求BC的长.
,求BC的长.
(1)可证明∠AEO=∠C=90°.即DE⊥AC.又OE为半圆O的半径,
∴AC是半圆O的切线.(2)BC=4.
解析试题分析:解:(1)连接OE。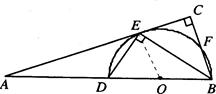
∵E为 的中点,
的中点,
∴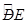 =
=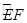 .
.
∴∠OBE=∠CBE.
∵OE=OB,
∴∠OEB=∠OBE.
∴∠OEB=∠CBE.
∴OE∥BC.
∵BC⊥AC,∴∠C=90°.
∴∠AEO=∠C=90°.即DE⊥AC.
又OE为半圆O的半径,
∴AC是半圆O的切线.
(2)设⊙O的半径为x
∵OE⊥AC,
∴(x+6)2-(6 )2=x2.
)2=x2.
∴x=3.
∴AB=AD+OD+OB=12.
∵OE∥BC,
∴△AOE~△ABC.
∴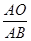 =
=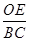
即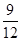 =
=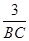
∴BC=4.。
考点:圆的切线性质与相似三角形
点评:本题难度较低,主要考查学生对圆的切线性质与相似三角形知识点的掌握。为中考常考题型,要求学生牢固掌握。

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
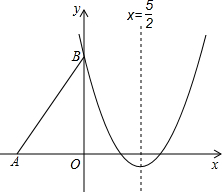 (2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
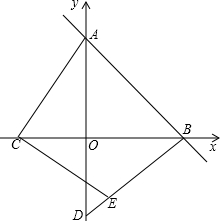
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=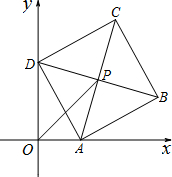 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
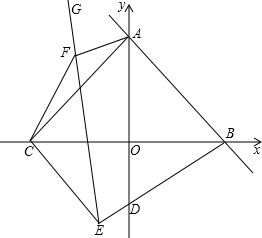
 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.