题目内容
如图，△ABC经过相似变换得△DEF．若∠ABC=20°，∠BCA=40°，AB：DE=2：1，则∠EDF的度数是________．
120°
分析：由相似变换可得△ABC∽△EDF，由相似三角形的性质：对应角相等即可求出∠EDF的度数．
解答：∵，△ABC经过相似变换得△DEF．
∴△ABC∽△EDF，
∵AB：DE=2：1，
∴∠BAC=∠EDF，
∵∠ABC=20°，∠BCA=40°，
∴∠EDF=∠BAC=180°-20°-40°=120°，
故答案为120°．
点评：本题考查了特殊的相似：位似，以及相似三角形的性质和三角形的内角和定理的运用，题目比较简单．
分析：由相似变换可得△ABC∽△EDF，由相似三角形的性质：对应角相等即可求出∠EDF的度数．
解答：∵，△ABC经过相似变换得△DEF．
∴△ABC∽△EDF，
∵AB：DE=2：1，
∴∠BAC=∠EDF，
∵∠ABC=20°，∠BCA=40°，
∴∠EDF=∠BAC=180°-20°-40°=120°，
故答案为120°．
点评：本题考查了特殊的相似：位似，以及相似三角形的性质和三角形的内角和定理的运用，题目比较简单．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
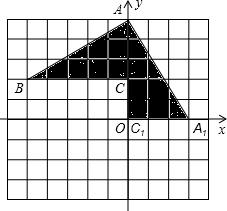如图，在平面直角坐标系中，有一直角△ABC，且A（0，5），B（-5，2），C（0，2），并已知△AA1C1是由△ABC经过旋转变换得到的．
点A和B不重合），以OA为半径的⊙O与AB相交于点E．
、
,斜边为
).
、
,斜边为
).
、
,斜边为
).