题目内容
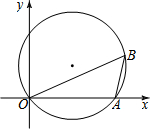 (2013•荆门模拟)如图,已知点A(8,0),sin∠ABO=
(2013•荆门模拟)如图,已知点A(8,0),sin∠ABO=| 4 |
| 5 |
分析:根据圆周角定理以及勾股定理和垂径定理得出E,F点着的坐标,进而利用顶点式求出抛物线解析式即可.
解答: 解:如图所示:连接AC,过圆心O′作EF⊥OA,
解:如图所示:连接AC,过圆心O′作EF⊥OA,
∵∠AOC=90°,∠ABO=∠OCA,
∴
=
,
∵点A(8,0),
∴AC=10,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴MF=2,
∴F点坐标为:(4,-2),
设过O,A,F的抛物线解析式为:y=a(x-4)2-2,
将A代入(8,0)得:
0=a(8-4)2-2,
解得:a=
,
∴此时抛物线解析式为:y=
(x-4)2-2=
x2-x,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴ME=8,
∴E点坐标为:(4,8),
设过O,A,E的抛物线解析式为:y=a(x-4)2+8,
将A代入(8,0)得:
0=a(8-4)2+8,
解得:a=-
,
∴此时抛物线解析式为:y=-
(x-4)2+8=-
x2+x,
故选:D.
 解:如图所示:连接AC,过圆心O′作EF⊥OA,
解:如图所示:连接AC,过圆心O′作EF⊥OA,∵∠AOC=90°,∠ABO=∠OCA,
∴
| AO |
| AC |
| 4 |
| 5 |
∵点A(8,0),
∴AC=10,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴MF=2,
∴F点坐标为:(4,-2),
设过O,A,F的抛物线解析式为:y=a(x-4)2-2,
将A代入(8,0)得:
0=a(8-4)2-2,
解得:a=
| 1 |
| 8 |
∴此时抛物线解析式为:y=
| 1 |
| 8 |
| 1 |
| 8 |
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴ME=8,
∴E点坐标为:(4,8),
设过O,A,E的抛物线解析式为:y=a(x-4)2+8,
将A代入(8,0)得:
0=a(8-4)2+8,
解得:a=-
| 1 |
| 2 |
∴此时抛物线解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:此题主要考查了利用顶点式求抛物线解析式以及垂径定理、圆周角定理、勾股定理的应用,根据已知得出E,F点坐标是解题关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
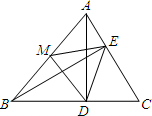 (2013•荆门模拟)已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°.则△EDM的面积为( )
(2013•荆门模拟)已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°.则△EDM的面积为( )