Question

【题目】若是边长为的等边三角形，点是的重心，连接延长至点，交于，，则四边形的周长为________．

Answer 1

【答案】

【解析】

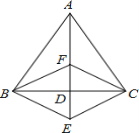
根据等边三角形的性质可知外心, 重心, 垂心三心合一; 且内角均为60; 根据勾股定理可求出AD的长, 利用重心的性质可求出DF的长, 再证明四边形BECF是菱形即可求出其周长.

解：ΔABC是边长为6的等边三角形, 点F是ΔABC的重心,

AB=BC=6, AD⊥BC,

BD=CD=BC=3,

AD==,

FD=AD=.

AD⊥BC, BD=CD,

BF=CF, BE=CE,∠BEF=∠CEF,

CF//BE,∠CFE=∠BEF, ∠CEF=∠CFE,

CF=CE,BE=CE=CF=BF,

四边形BECF是菱形,

BD=3,DF=,

BF= =,

四边形BECF的周长是4 =.

故答案为: .