题目内容
 已知:如图,AB=m(m>0),∠BAC=α(α为锐角),在射线AC上取一点D.使构成的△ABD恰好有两种,则线段BD的取值范围是
已知:如图,AB=m(m>0),∠BAC=α(α为锐角),在射线AC上取一点D.使构成的△ABD恰好有两种,则线段BD的取值范围是m•sinα<BD<m
m•sinα<BD<m
.分析:首先过点B作BE⊥AC于点E,由AB=m(m>0),∠BAC=α(α为锐角),利用三角函数的定义,即可求得BE的长,又由在射线AC上取一点D.使构成的△ABD恰好有两种,即可求得线段BD的取值范围.
解答: 解:过点B作BE⊥AC于点E,
解:过点B作BE⊥AC于点E,
∵AB=m(m>0),∠BAC=α(α为锐角),
∴BE=AB•sinα=m•sinα,
∵在射线AC上取一点D.使构成的△ABD恰好有两种,
∴线段BD的取值范围是:m•sinα<BD<m.
故答案为:m•sinα<BD<m.
 解:过点B作BE⊥AC于点E,
解:过点B作BE⊥AC于点E,∵AB=m(m>0),∠BAC=α(α为锐角),
∴BE=AB•sinα=m•sinα,
∵在射线AC上取一点D.使构成的△ABD恰好有两种,
∴线段BD的取值范围是:m•sinα<BD<m.
故答案为:m•sinα<BD<m.
点评:此题考查了解直角三角形的应用.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.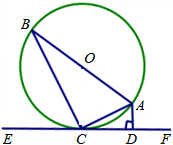 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.