Question

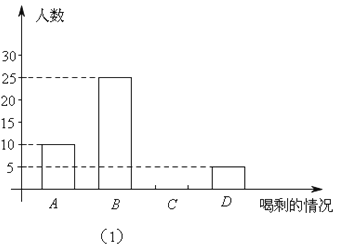
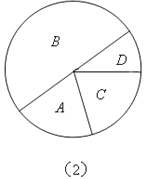
【题目】为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):

身高情况分组表(单位:cm)

组别	身高
A	x＜155
B	155≤x＜160
C	160≤x＜165
D	165≤x＜170
E	x≥170

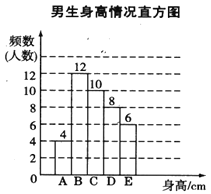
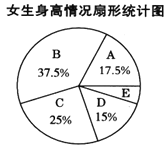
根据图表提供的信息,回答下列问题:

(1)样本中,男生身高的众数在___________组,中位数在___________组；

(2)样本中,女生身高在E组的有___________人；

(3)已知该校共有男生400人、女生380人,请估计身高在160≤x＜170范围内的学生约有多少人.

Answer 1

【答案】（1）B，C；（2）2；（3）332.

【解析】试题分析：（1）根据众数的定义，以及中位数的定义解答即可；
（2）先求出女生身高在E组所占的百分比，再求出总人数然后计算即可得解；
（3）分别用男、女生的人数乘以C、D两组的频率的和，计算即可得解．

试题解析：

∵B组人数最多，
∴众数在B组，
男生总人数为4+12+10+8+6=40，
按照从低到高的顺序，第20、21两人都在C组，
∴中位数在C组，
故答案为：B、C；
（2）女生身高在E组的频率为：1-17.5%-37.5%-25%-15%=5%，
∵抽取的样本中，男生、女生的人数相同，
∴样本中，女生身高在E组的人数有40×5%=2人，
故答案为：2；
（3）400× +380×（25%+15%）=180+152=332（人）．

答：估计该校身高在160≤x＜170之间的学生约有332人．