题目内容
【题目】已知抛物线![]() (b,c为常数)经过点
(b,c为常数)经过点![]() .
.
(1)求抛物线的解析式;
(2)设该抛物线与x轴的另一个交点为C,其顶点为D,求点C,D的坐标,并判断![]() 形状;
形状;
(3)点P是直线![]() 上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线
上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线![]() 上,距离点P为
上,距离点P为![]() 个单位长度.设点P的横坐标为t,
个单位长度.设点P的横坐标为t,![]() 的面积为S,求S与t之间的函数关系式.
的面积为S,求S与t之间的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,直角三角形;(3)当点M在点P下方时,
,直角三角形;(3)当点M在点P下方时,![]() ,当点M在点P上方时,
,当点M在点P上方时,![]() (
(![]() 或
或![]() )
)
【解析】
(1)利用待定系数法即可求得答案;
(2)将二次函数关系式配成顶点式即可求得顶点D的坐标,令y=0即可求得点C的坐标,最后利用该勾股定理及其逆定理即可判断![]() 的形状;
的形状;
(3)过点Q作![]() 于点G.先求得
于点G.先求得![]() ,再根据点P的位置分类讨论,画出相应图形计算即可.
,再根据点P的位置分类讨论,画出相应图形计算即可.
解:(1)∵抛物线过![]() 两点,
两点,
∴![]()
解得![]()
∴抛物线解析式为![]() ;
;
(2)由![]() ,得点D的坐标为
,得点D的坐标为![]() .
.
当![]() 时,
时,![]() ,
,
解得![]() .
.
∴点C的坐标为![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 为直角三角形.
为直角三角形.
(3)过点Q作![]() 于点E.
于点E.
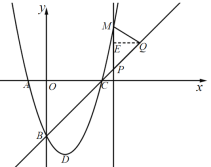
∵![]() 轴,
轴,
∴![]() .
.
∵![]() ,
,
∴![]() ,直线
,直线![]() 的解析式为
的解析式为![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
①当点M在点P下方时,![]() ,
,
∴![]() .
.
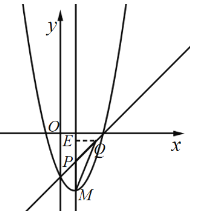
②当点M在点P上方时,![]() ,
,
∴![]() (
(![]() 或
或![]() )
)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目