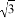题目内容
4.先化简,再求值:$\frac{x-2}{x-1}$÷(x+1-$\frac{3}{x-1}$),其中x=tan60°-2.分析 利用通分与合并同类项等方法将原分式进行化简,再将x=tan60°-2=$\sqrt{3}$-2代入到化简后的分式中,即可求出结论.
解答 解:原式=$\frac{x-2}{x-1}÷\frac{{x}^{2}-1-3}{x-1}$
=$\frac{x-2}{x-1}×\frac{x-1}{(x+2)(x-2)}$
=$\frac{1}{x+2}$.
当x=tan60°-2=$\sqrt{3}$-2时,原式=$\frac{1}{\sqrt{3}-2+2}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了分式的化简求值,解题的关键是将原分式化简成$\frac{1}{x+2}$.本题属于基础题,难度不大,解决该题型题目时,先将原式进行化简,再代入数据求值.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
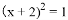 B.
B. 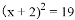
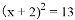 D.
D. 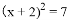
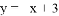 与
与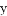 轴交于点A,与反比例函数
轴交于点A,与反比例函数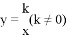 的图像交于点C,过点C作CB⊥
的图像交于点C,过点C作CB⊥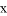 轴于点B,AO=3BO,则反比例函数的解析式为( )
轴于点B,AO=3BO,则反比例函数的解析式为( )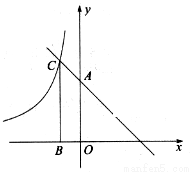
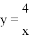 B.
B. 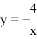 C.
C. 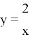 D.
D. 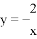
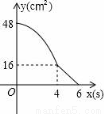 B.
B. 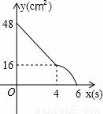 C.
C. 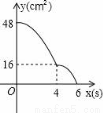 D.
D. 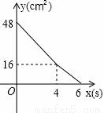
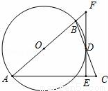
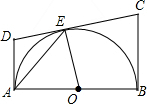 如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )
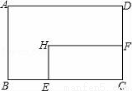
如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )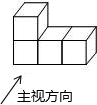 如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积.
如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积. 从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱.
从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱. B.
B. 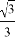 C.
C.  D.
D.