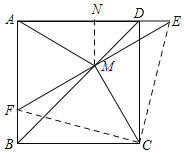
题目内容
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
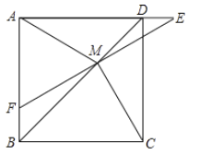
A.①②③B.①②④C.②③④D.①②③④
【答案】A
【解析】
①证明△AFM是等边三角形,可判断; ②③证明△CBF≌△CDE(ASA),可作判断; ④设MN=x,分别表示BF、MD、BC的长,可作判断.
解:①∵AM=EM,∠AEM=30°, ∴∠MAE=∠AEM=30°,
∴∠AMF=∠MAE+∠AEM=60°,
∵四边形ABCD是正方形, ∴∠FAD=90°,
∴∠FAM=90°-30°=60°,
∴△AFM是等边三角形,
∴FM=AM=EM, 故①正确;
②连接CE、CF, ∵四边形ABCD是正方形, ∴∠ADB=∠CDM,AD=CD,
在△ADM和△CDM中,
∵ 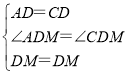 ,
,
∴△ADM≌△CDM(SAS), ∴AM=CM,
∴FM=EM=CM, ∴∠MFC=∠MCF,∠MEC=∠ECM,
∵∠ECF+∠CFE+∠FEC=180°, ∴∠ECF=90°,
∵∠BCD=90°, ∴∠DCE=∠BCF,
在△CBF和△CDE中,
∵ 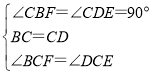 ,
,
∴△CBF≌△CDE(ASA), ∴BF=DE; 故②正确;
③∵△CBF≌△CDE, ∴CF=CE, ∵FM=EM, ∴CM⊥EF, 故③正确;
④过M作MN⊥AD于N, 设MN=![]() ,则AM=AF=
,则AM=AF=![]() ,
,

![]() ,DN=MN=
,DN=MN=![]() , ∴AD=AB=
, ∴AD=AB= ![]() ,
,
∴DE=BF=AB-AF=![]() ,
,
∴ ![]() ,
,
∵BC=AD= ![]() , 故④错误;
, 故④错误;
所以本题正确的有①②③;
故选:A.

练习册系列答案
相关题目