题目内容

如图，△ABC中，∠A=30°，∠B=45°，AB=6cm，动点P从A点以 $数学公式$ cm/s匀速向C点运动，动点Q同时从B点以2cm/s匀速向A点运动，一点运动到终点时另一点也随之停止．

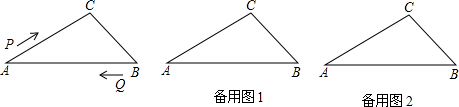
（1）求P点从A点运动到C点需要的时间t；
（2）试求出当t为何值时△APQ为直角三角形？

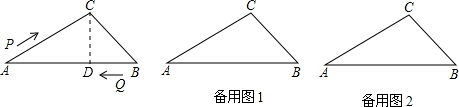解：（1）过点C作CD⊥AB于D．设CD=x．
在Rt△ACD中，∵∠ADC=90°，∠A=30°，
∴AD= $\text{[math]}$ x，AC=2x；
在Rt△BCD中，∵∠BDC=90°，∠B=45°，
∴BD=x；
∵AD+BD=AB，
∴ $\text{[math]}$ x+x=6，
解得x=3 $\text{[math]}$ -3，
∴AC=2x=6 $\text{[math]}$ -6，
∵动点P从A点以 $\text{[math]}$ cm/s匀速向C点运动，
∴P点从A点运动到C点需要的时间t= 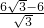$\text{[math]}$ =6-2 $\text{[math]}$ ；

（2）由题意，知AP= $\text{[math]}$ t，BQ=2t，
∴AQ=AB-BQ=6-2t．
当△APQ为直角三角形时，分两种情况：
①如果∠APQ=90°，cos30°= $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
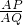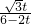解得t₁= $\text{[math]}$ ；
②如果∠AQP=90°，cos30°= $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
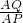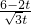解得t₂= $\text{[math]}$ ．
因为它们均小于6-2 $\text{[math]}$ ，故都成立．
故当t为 $\text{[math]}$ 秒或 $\text{[math]}$ 秒时，△APQ为直角三角形．
分析：（1）过点C作CD⊥AB于D．设CD=x，则AD= $\text{[math]}$ x，AC=2x，BD=x，根据AD+BD=AB，列出方程，解方程求出x的值，得到AC的长，然后根据时间=÷速度即可求解；
求得AC=6 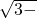$\text{[math]}$ 6，故t=6-2 $\text{[math]}$ 秒
（2）当△APQ为直角三角形时，分两种情况：①∠APQ=90°；②∠AQP=90°；根据余弦函数的定义求解即可．
点评：本题考查了解直角三角形，难度适中，准确作出辅助线是解题的关键．