题目内容
【题目】已知:等边三角形![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
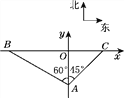
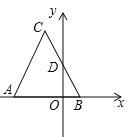
(1)如图,求![]() 、
、![]() 的坐标及
的坐标及![]() 的长;
的长;
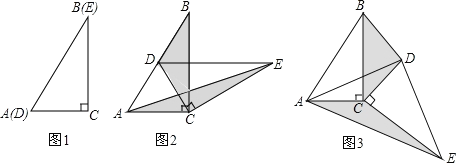
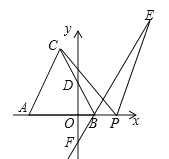
(2)如图,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是
是![]() 右侧一点,
右侧一点,![]() ,且
,且![]() .连接
.连接![]() .
.
求证:直线![]() 必过点
必过点![]() 关于
关于![]() 轴对称的对称点;
轴对称的对称点;
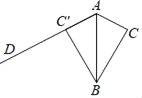
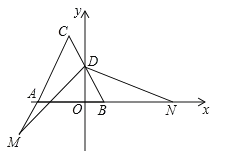
(3)如图,若点![]() 在
在![]() 延长线上,点
延长线上,点![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)A(-3,0),B(1,0),CD=2;(2)见解析;(3)6.
【解析】
(1)首先利用绝对值的非负性得出![]() ,即可得出点A、B的坐标;得出AB、BC,然后由∠CBA=60°得出∠ODB=30°,进而得出BD,得出CD;
,即可得出点A、B的坐标;得出AB、BC,然后由∠CBA=60°得出∠ODB=30°,进而得出BD,得出CD;
(2)首先判定△CEP、△ABC为等边三角形,进而判定△CBE≌△CAP,然后利用角和边的关系得出DO=OF,即可判定点D、F关于![]() 轴对称,直线
轴对称,直线![]() 必过点
必过点![]() 关于
关于![]() 轴对称的对称点;
轴对称的对称点;
(3)作DI∥AB,判定△CDI为等边三角形,然后判定△MDI≌△NDB,得出NB=MI,进而得出![]() 的值.
的值.
(1)∵![]() ,即
,即![]()
∴![]()
∴![]()
∴A(-3,0),B(1,0),
∴AB=BC=4,
∵∠CBA=60°
∴∠ODB=30°
∴BD=2OB=2
∴CD=BC-BD=4-2=2;
(2)延长EB交![]() 轴于F,连接CE,如图所示:
轴于F,连接CE,如图所示:

∵![]() ,
,![]()
∴△CEP为等边三角形
∴∠ECP=60°,CE=CP
由(1)中得知,△ABC为等边三角形
∴∠ACB=60°,CA=CB
∴∠ACB+∠BCP=∠ECP+∠BCP
∴∠ACP=∠BCE
∴△CBE≌△CAP(SAS)
∴∠CEB=∠CPA
∴∠EBP=∠ECP=60°
∴∠FBO=∠DBO=60°
∴∠BFO=∠BDO=30°
∴BD=BF
∵BO⊥DF
∴DO=OF
∴点D、F关于![]() 轴对称
轴对称
∴直线![]() 必过点
必过点![]() 关于
关于![]() 轴对称的对称点;
轴对称的对称点;
(3)过点D作DI∥AB交AC于I,如图所示:

由(2)中△ABC为等边三角形,则△CDI为等边三角形,
∴DI=CD=DB
∴∠MID=120°=∠DBN
∴△MDI≌△NDB(AAS)
∴NB=MI
∴AN-AM=(AB+NB)-AM=AB+MI-AM=AB+AI=AB+BD=4+2=6