题目内容
如图所示,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是 上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.
上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.(1)求证:DM=
 r;
r;(2)求证:直线PC是扇形OAB所在圆的切线;
(3)设y=CD2+3CM2,当∠CPO=60°时,请求出y关于r的函数关系式.

【答案】分析:(1)连接OC,由CD⊥OA于点D,CE⊥OB于点E,证明四边形ODCE是矩形,
(2)设OC与DE交于点F,则在矩形ODCE中,FC=FD,根据角的关系得到PC⊥OC于点C,
(3)过C作CH⊥DE于点H,在Rt△OCD和Rt△CDH中解得CD、DH、CH,进而写出y关于r的函数关系式.
解答: (1)证明:连接OC,
(1)证明:连接OC,
∵点C是 上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,
上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,
∴∠ODC=∠OEC=∠AOB=90°,
∴四边形ODCE是矩形,
∴DE=OC.
∵OC=OA=r,
∴DE=r.
又∵DM=2EM,
∴DM= DE=
DE= r;
r;
(2)证明:设OC与DE交于点F,则在矩形ODCE中,FC=FD,
∴∠CDE=∠DCO,
又∵∠CPD+∠PCD=90°,∠CPD=∠CDE,
∴∠DCO+∠PCD=90°,即PC⊥OC于点C,
又∵OC为扇形OAB的半径,
∴PC是扇形OAB所在圆的切线;
(3)解:过C作CH⊥DE于点H
∵∠OCD=∠CDH=∠CPO=60°,
∴在Rt△OCD和Rt△CDH中,得
CD= OC=
OC= r,DH=
r,DH= CD=
CD= r,CH=
r,CH= r.
r.
又MH=DM-DH= r-
r- r=
r= r,
r,
∴在Rt△CMH中,得CM2=MH2+CH2= ,
,
则y=CD2+3CM2,
= +3×
+3× r2
r2
= r2.
r2.
点评:本题考查了切线的判定,勾股定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
(2)设OC与DE交于点F,则在矩形ODCE中,FC=FD,根据角的关系得到PC⊥OC于点C,
(3)过C作CH⊥DE于点H,在Rt△OCD和Rt△CDH中解得CD、DH、CH,进而写出y关于r的函数关系式.
解答:
 (1)证明:连接OC,
(1)证明:连接OC,∵点C是
 上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,
上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,∴∠ODC=∠OEC=∠AOB=90°,
∴四边形ODCE是矩形,
∴DE=OC.
∵OC=OA=r,
∴DE=r.
又∵DM=2EM,
∴DM=
 DE=
DE= r;
r;(2)证明:设OC与DE交于点F,则在矩形ODCE中,FC=FD,
∴∠CDE=∠DCO,
又∵∠CPD+∠PCD=90°,∠CPD=∠CDE,
∴∠DCO+∠PCD=90°,即PC⊥OC于点C,
又∵OC为扇形OAB的半径,
∴PC是扇形OAB所在圆的切线;
(3)解:过C作CH⊥DE于点H
∵∠OCD=∠CDH=∠CPO=60°,
∴在Rt△OCD和Rt△CDH中,得
CD=
 OC=
OC= r,DH=
r,DH= CD=
CD= r,CH=
r,CH= r.
r.又MH=DM-DH=
 r-
r- r=
r= r,
r,∴在Rt△CMH中,得CM2=MH2+CH2=
 ,
,则y=CD2+3CM2,
=
 +3×
+3× r2
r2=
 r2.
r2.点评:本题考查了切线的判定,勾股定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

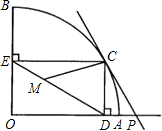 点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.
点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.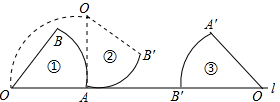 到图③,∠O=60°,OA=1.
到图③,∠O=60°,OA=1. 上,AF⊥ED,交ED的延长线于点F.如果正方形的边长为2,则图中阴影部分的面积是( )
上,AF⊥ED,交ED的延长线于点F.如果正方形的边长为2,则图中阴影部分的面积是( )
 )平方单位 B.2(
)平方单位 B.2( )平方单位
D.2(
)平方单位
D.2( 上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.
上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE. r;
r;