题目内容
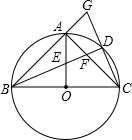
23、如图，⊙O以等腰△ABC的一腰AB为直径，它交另一腰AC于E，交BC于D．求证：BC=2DE．
分析：连接AD，利用等腰三角形三线合一的性质，可证得BB=DC，因为四边形ABDE是圆内接四边形，所以∠CED=∠B，又∠B=∠C，所以∠CED=∠C，所以DE=DC，所以BC=2DC=2DE．
解答：解：
连接AD，
∵AB是⊙O的直径，
∴∠ADB=90°，
又∵AB=AC，
∴∠B=∠C，BD=DC，即BC=2DC，
∵四边形ABDE是圆内接四边形，
∴∠CED=∠B，
又∠B=∠C，
∴∠CED=∠C，
∴DE=DC，
∴BC=2DE．
连接AD，∵AB是⊙O的直径，
∴∠ADB=90°，
又∵AB=AC，
∴∠B=∠C，BD=DC，即BC=2DC，
∵四边形ABDE是圆内接四边形，
∴∠CED=∠B，
又∠B=∠C，
∴∠CED=∠C，
∴DE=DC，
∴BC=2DE．
点评：本题综合考查了等腰三角形的性质和与圆有关一些性质定理，题目典型，中等难度，考查知识面广．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
如图，分别以等腰直角三角板的直角边、斜边为旋转轴旋转，所形成的旋转体的全面积依次记为S1，S2，则S1与S2的大小关系为（ ）| A、S1＞S2 | B、S1＜S2 | C、S1=S2 | D、无法判断 |
AC分别交于点E、F延长BA、CD交于G．
