题目内容
 填空(如图):
填空(如图):
在上图中:①∠1=∠2,理由是________.
②如果a∥b,那么∠1与∠4的关系是________,理由是________.
③如果a∥b,那么∠2与∠4的关系是________,理由是________.
④如果a∥b,那么∠2与∠3的关系是________,理由是________.
对顶角相等 ∠1=∠4 两直线平行,同位角相等 ∠2=∠4 两直线平行,内错角相等 ∠2+∠3=180° 两直线平行,同旁内角互补
分析:①根据对顶角的定义即可解答;
②根据两条平行线被第三条直线所截,同位角相等即可解答;
③根据两条平行线被第三条直线所截,内错角相等即可解答;
④根据两条平行线被地三条直线所截,同旁内角互补即可解答.
解答: 解:如图,
解:如图,
①∵∠1和∠2是对顶角,
∴∠1=∠2(对顶角相等);
②∵a∥b,∠1和∠4是同位角,
∴∠1=∠4(两直线平行,同位角相等);
③∵a∥b,∠2和∠4是内错角,
∴∠2=∠4(两直线平行,内错角相等);
④∵a∥b,∠2和∠3是同旁内角,
∴∠2+∠3=180°(两直线平行,同旁内角互补).
故答案为:①对顶角相等;②∠1=∠4;两直线平行,同位角相等;③∠2=∠4;两直线平行,内错角相等;④∠2+∠3=180°;两直线平行,同旁内角互补.
点评:本题主要考查了平行线的性质:两条平行线被第三条直线所截,同位角相等;两条平行线被第三条直线所截,内错角相等;两条平行线被地三条直线所截,同旁内角互补.
分析:①根据对顶角的定义即可解答;
②根据两条平行线被第三条直线所截,同位角相等即可解答;
③根据两条平行线被第三条直线所截,内错角相等即可解答;
④根据两条平行线被地三条直线所截,同旁内角互补即可解答.
解答:
 解:如图,
解:如图,①∵∠1和∠2是对顶角,
∴∠1=∠2(对顶角相等);
②∵a∥b,∠1和∠4是同位角,
∴∠1=∠4(两直线平行,同位角相等);
③∵a∥b,∠2和∠4是内错角,
∴∠2=∠4(两直线平行,内错角相等);
④∵a∥b,∠2和∠3是同旁内角,
∴∠2+∠3=180°(两直线平行,同旁内角互补).
故答案为:①对顶角相等;②∠1=∠4;两直线平行,同位角相等;③∠2=∠4;两直线平行,内错角相等;④∠2+∠3=180°;两直线平行,同旁内角互补.
点评:本题主要考查了平行线的性质:两条平行线被第三条直线所截,同位角相等;两条平行线被第三条直线所截,内错角相等;两条平行线被地三条直线所截,同旁内角互补.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
为缓解油价上涨给出租车行业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数).
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD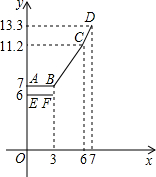 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= ;
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD
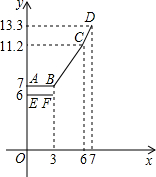 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 | |
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
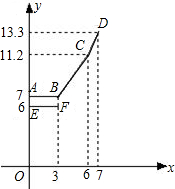 为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 |
①填空:a=
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a=______,b=______,c=______.
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.

| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 |
①填空:a=______,b=______,c=______.
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.

 填空(如图):
填空(如图):