题目内容
 如图,已知A(a,0)、B(0,b),且a、b满足
如图,已知A(a,0)、B(0,b),且a、b满足| a-5 |
(1)△BOD与△AOC全等吗?为什么?
(2)若点C的纵坐标为2,求四边形AODB的面积.
考点:全等三角形的判定,坐标与图形性质,三角形的面积,等腰直角三角形
专题:
分析:(1)根据非负数的性质求得a=b=5,易证△AOB是等腰直角三角形.由全等三角形的判定定理SAS证得结论;
(2)利用(1)中全等三角形的性质可以推知四边形AODB的面积=等腰直角△AOB的面积.
(2)利用(1)中全等三角形的性质可以推知四边形AODB的面积=等腰直角△AOB的面积.
解答: 解:(1)△BOD与△AOC全等.理由如下:
解:(1)△BOD与△AOC全等.理由如下:
∵
+a2-2ab+b2=0=
+(a-b)2=0,
∴a=5,b=a=5,
∴A(5,0)、B(0,5),
∴OA=OB=5.
∵∠COD═∠AOB=90°,
∴∠DOB=∠COA.
∵在△BOD与△AOC中,
,
∴△BOD≌△AOC(SAS),即△BOD与△AOC全等;
(2)由(1)知,△BOD≌△AOC,则S△BOD=S△AOC,
∴S四边形AODB=S△AOB=
OA•OB=
.
 解:(1)△BOD与△AOC全等.理由如下:
解:(1)△BOD与△AOC全等.理由如下:∵
| a-5 |
| a-5 |
∴a=5,b=a=5,
∴A(5,0)、B(0,5),
∴OA=OB=5.
∵∠COD═∠AOB=90°,
∴∠DOB=∠COA.
∵在△BOD与△AOC中,
|
∴△BOD≌△AOC(SAS),即△BOD与△AOC全等;
(2)由(1)知,△BOD≌△AOC,则S△BOD=S△AOC,
∴S四边形AODB=S△AOB=
| 1 |
| 2 |
| 25 |
| 2 |
点评:本题考查了坐标与图形性质,三角形的面积以及等腰直角三角形.根据非负数的性质求得OB=OA是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
下列不是二次函数的是( )
| A、y=3(x-1)2-1 | ||
B、y=
| ||
C、y=
| ||
| D、y=(x+1)(x-1) |
整式5m2-3m-5减去整式-3m所得的结果是( )
| A、5(m2-1) |
| B、5m2-6m-5 |
| C、5(m2+1) |
| D、-(5m2+6m-5) |
下列结论正确的是( )
| A、64的立方根是±4 | ||||||
B、-
| ||||||
| C、立方根等于本身的数是0 | ||||||
D、
|
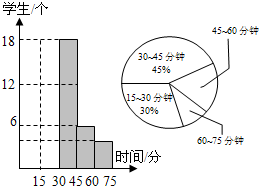 为了了解学校推行素质教育情况,市教育对某个学校七年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
为了了解学校推行素质教育情况,市教育对某个学校七年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题: 如图,AD=AE,∠B=∠C,BD与CE相交于点G,求证:BG=GC.
如图,AD=AE,∠B=∠C,BD与CE相交于点G,求证:BG=GC.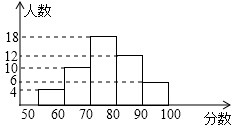 某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题:
某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题: 如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠C=45°,BC=4,AD=2.求四边形ABCD的面积.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠C=45°,BC=4,AD=2.求四边形ABCD的面积.