题目内容
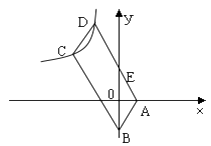
【题目】正方形ABCD、正方形BEFG和正方形DMNK的位置如图所示,点A在线段NF上,AE=8,则△NFP的面积为( ).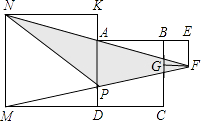
A.30
B.32
C.34
D.36
【答案】B
【解析】四边形BEFG、DMNK、ABCD是正方形,
∴∠E=∠F=90,AE∥MC,MC∥NK,
∴AE∥NK,
∴∠KNA=∠EAF,
∴△KNA∽△EAF,
∴NK:EA=KA:EF,
设BE=x,则AB=8x,NK=y,KA=y(8x)=x+y8,
∴![]() =
=![]()
∴![]() =
=![]() +1,
+1,
观察可知:当y=8时,等式成立,
∴y=8,
∴NK=AE,
∴△KNA≌△EAF,
∴NA=AF
∴FP=PM,
∴S△MNP=S△NPF,
∴S正方形DMNK=2S△MNP=64,
∴S△MNP=32,
∴S△NPF=32.
所以答案是:B.
【考点精析】本题主要考查了平行线的判定与性质和正方形的性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目