题目内容
已知函数y1=ax2+bx+c,y2=ax+b(a>b>c),当x=1时,y1=0.
(Ⅰ)证明:y1与y2的图象有2个交点;
(Ⅱ)设y1与y2的图象交点A,B在x轴上的射影为A1,B1,求|A1B1|的取值范围.
解:(1)当自变量x=1时函数值为0,将其代入y1中得到
y1=a+b+c=0,又有a>b>c,可知,a>0,c<0,b的正负不能确定,
联系两个函数,即两线相交:ax2+bx+c=ax+b,
ax2+(b-a)x+(c-b)=0,
△=(b-a)2-4a(c-b)=(b-a)2-4ac+4ab=(b+a)2-4ac,
∵a>0,c<0,-4ac>0,
∴(b+a)2-4ac>0,
∴两个函数图象必有两个不同的交点;
(2)上述两函数图象的交点A.B在x轴上的射影分别为A1.B1,
根据A1,B1为ax2+bx+c=ax+b的两根,
ax2+(b-a)x+(c-b)=0
有两根为
x1= ,x2=
,x2=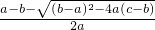 ,
,
A1B1=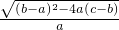
=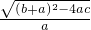
=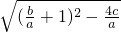 ,
,
∵-c=a+b,
∴A1B1=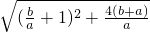
=
=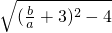 .
.
由a>b,a>0,有 >
> ,
,
即1> ,
,
由-a=b+c,b>c,得到-a=b+c<2b,
即-a<2b,得到 >-
>- ,
,
∴ <
< <1分别代入A式为,
<1分别代入A式为,
∴ <A1B1<2
<A1B1<2  .
.
分析:(1)将两个解析式组成一个方程组后,然后转化为一个一元二次方程,由根的判别式就可以得出结论.
(2)由条件利用求根公式可以表示出A1、B1的横坐标,由数轴上的点表示出A1B1的值,确定出 的取值范围,从而确定出A1B1的范围,得出结论.
的取值范围,从而确定出A1B1的范围,得出结论.
点评:此题考查了抛物线与x轴的交点,根的判别式,勾股定理的运用,函数值的运用及韦达定理的运用,利用韦达定理得出|A1B1|的取值范围是解题关键.
y1=a+b+c=0,又有a>b>c,可知,a>0,c<0,b的正负不能确定,
联系两个函数,即两线相交:ax2+bx+c=ax+b,
ax2+(b-a)x+(c-b)=0,
△=(b-a)2-4a(c-b)=(b-a)2-4ac+4ab=(b+a)2-4ac,
∵a>0,c<0,-4ac>0,
∴(b+a)2-4ac>0,
∴两个函数图象必有两个不同的交点;
(2)上述两函数图象的交点A.B在x轴上的射影分别为A1.B1,
根据A1,B1为ax2+bx+c=ax+b的两根,
ax2+(b-a)x+(c-b)=0
有两根为
x1=
 ,x2=
,x2=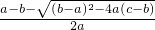 ,
,A1B1=
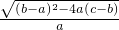
=
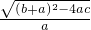
=
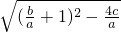 ,
,∵-c=a+b,
∴A1B1=
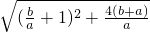
=

=
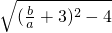 .
. 由a>b,a>0,有
 >
> ,
,即1>
 ,
,由-a=b+c,b>c,得到-a=b+c<2b,
即-a<2b,得到
 >-
>- ,
,∴
 <
< <1分别代入A式为,
<1分别代入A式为,∴
 <A1B1<2
<A1B1<2  .
.分析:(1)将两个解析式组成一个方程组后,然后转化为一个一元二次方程,由根的判别式就可以得出结论.
(2)由条件利用求根公式可以表示出A1、B1的横坐标,由数轴上的点表示出A1B1的值,确定出
 的取值范围,从而确定出A1B1的范围,得出结论.
的取值范围,从而确定出A1B1的范围,得出结论.点评:此题考查了抛物线与x轴的交点,根的判别式,勾股定理的运用,函数值的运用及韦达定理的运用,利用韦达定理得出|A1B1|的取值范围是解题关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 已知函数y1=ax2+bx+c,其中a<0,b>0,c>0,问:
已知函数y1=ax2+bx+c,其中a<0,b>0,c>0,问: 已知函数y1=ax2+bx+c(a≠0)和y2=mx+n的图象交于(-2,-5)点和(1,4)点,并且y1=ax2+bx+c的图象与y轴交于点(0,3).
已知函数y1=ax2+bx+c(a≠0)和y2=mx+n的图象交于(-2,-5)点和(1,4)点,并且y1=ax2+bx+c的图象与y轴交于点(0,3).