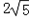题目内容
直线y=-x与直线y=-x+1之间的距离是分析：作出图形，根据k=-1可得两直线与坐标轴的夹角为45°，利用45°角的正弦值求解即可．
解答：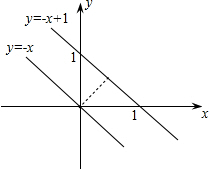
解：∵k=-1，
∴两直线与坐标轴的夹角的锐角是45°，
又∵直线y=-x+1，x=0时，y=1，
∴直线y=-x与直线y=-x+1之间的距离是：1×sin45°=
．
故答案为：
．
解：∵k=-1，∴两直线与坐标轴的夹角的锐角是45°，
又∵直线y=-x+1，x=0时，y=1，
∴直线y=-x与直线y=-x+1之间的距离是：1×sin45°=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了两条直线的平行问题，根据k=-1得到直线与坐标轴的夹角是45°是解题的关键．
练习册系列答案
相关题目
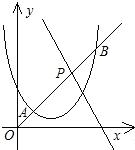已知抛物线y=x2-2x+6-m与直线y=-2x+6+m，它们的一个交点的纵坐标是4．
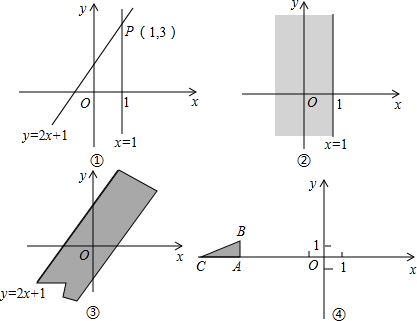右运动，当点A到达何位置时，小车被阴影部分挡住的面积最大？
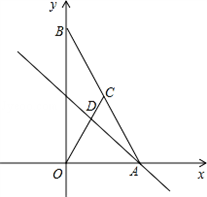
x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．
的解，点C是直线y=2x与直线AB的交点，点D在线段OC上，OD=
