题目内容
直角梯形ABCD中,AB∥CD,∠A=30°,AB+CD=m,BC+AD=n,则梯形ABCD的面积为
- A.

- B.

- C.

- D.

C
分析:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.根据三角函数可求得DE,BC的长,再利用面积公式即可求得梯形的面积.
解答: 解:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.
解:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.
在直角三角形ADE中,∵∠A=30°,
∴DE= AD即BC=
AD即BC= AD,
AD,
又∵BC+AD=n,
∴BC= n,
n,
根据梯形的面积公式,得它的面积= m•
m• n=
n= mn.
mn.
故选C.
点评:注意梯形中常见的辅助线之一:作高.此题中作高构造了一个矩形和一个30°直角三角形,能够根据直角三角形的性质进行计算.
分析:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.根据三角函数可求得DE,BC的长,再利用面积公式即可求得梯形的面积.
解答:
 解:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.
解:作梯形的另一高DE⊥AB于E,则四边形BCDE是矩形.在直角三角形ADE中,∵∠A=30°,
∴DE=
 AD即BC=
AD即BC= AD,
AD,又∵BC+AD=n,
∴BC=
 n,
n,根据梯形的面积公式,得它的面积=
 m•
m• n=
n= mn.
mn.故选C.
点评:注意梯形中常见的辅助线之一:作高.此题中作高构造了一个矩形和一个30°直角三角形,能够根据直角三角形的性质进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
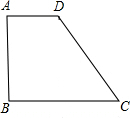 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为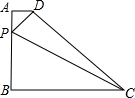 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为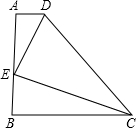 下结论:
下结论: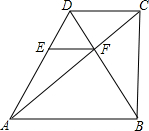 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.