Question

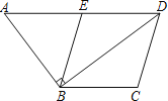
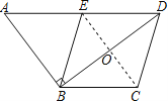
【题目】如图，四边形ABCD中，AD∥BC，AD=2BC，E为AD的中点，∠ABD=90°．

（1）求证：四边形BCDE是菱形；

（2）连接CE，若CE=6，BC=5，求四边形ABCD的面积．

Answer 1

【答案】（1）见解析；（2）36

【解析】

（1）根据已知条件得到四边形BCDE是平行四边形，根据直角三角形的性质得到BE=DE，于是得到结论；

（2）连接CE交BD于点O，由菱形的性质得到BD⊥CE于点O，OE=OC=CE=3，根据勾股定理得到BD=，由三角形的面积公式即可得到结论．

（1）证明：∵AD=2BC，E为AD的中点，

∴DE=BC，

∵AD∥BC，

∴四边形BCDE是平行四边形，

∵∠ABD=90°，E为AD的中点，

∴BE=DE，

∴四边形BCDE是菱形；

（2）解：如图，连接CE交BD于点O，

∵四边形BCDE是菱形，

∴BD⊥CE于点O，OE=OC=CE=3，

∵E为AD的中点，

∴OE∥AB，且AB=2OE=6，

在Rt△ABD中，∠ABD=90°，AD=2BC=10，AB=6，

∴BD===8，

∴△ABD的面积S△ABD=×AB×BD=×6×8=24，

△BCD的面积S△BCD=×BD×OC=×8×3=12，

∴四边形ABCD的面积S=S△ABD+S△BCD=36．