题目内容
如果
-
与1-
互为相反数,且x满足方程ax-3=a+x,求a的值.
| x+3 |
| 2 |
| x-7 |
| 6 |
| 2x+1 |
| 3 |
考点:解一元一次方程,一元一次方程的解
专题:
分析:
-
与1-
互为相反数,可得
-
+1-
=0,解得x的值代入方程ax-3=a+x,求a的值即可.
| x+3 |
| 2 |
| x-7 |
| 6 |
| 2x+1 |
| 3 |
| x+3 |
| 2 |
| x-7 |
| 6 |
| 2x+1 |
| 3 |
解答:解:由题意得
-
+1-
=0,
去分母,得3(x+3)-(x-7)+6-2(2x+1)=0
去括号,得3x+9-x+7+6-4x-2=0
移项,得3x-x-4x=-9-7-6+2
合并,得-2x=-20
系数化为1,得x=10,
把x=10代入ax-3=a+x得10a-3=a+10
解得a=
.
| x+3 |
| 2 |
| x-7 |
| 6 |
| 2x+1 |
| 3 |
去分母,得3(x+3)-(x-7)+6-2(2x+1)=0
去括号,得3x+9-x+7+6-4x-2=0
移项,得3x-x-4x=-9-7-6+2
合并,得-2x=-20
系数化为1,得x=10,
把x=10代入ax-3=a+x得10a-3=a+10
解得a=
| 13 |
| 9 |
点评:本题考查了解一元一次方程以及一元一次方程的解,解一元一次方程常见的过程有去括号、移项、系数化为1等.

练习册系列答案
相关题目
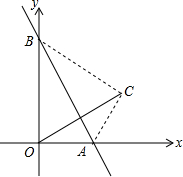 如图,直线y=-2x+10与x轴、y轴分别交于A、B两点,把△AOB沿AB翻折,点O落在点C处,求点C的坐标.
如图,直线y=-2x+10与x轴、y轴分别交于A、B两点,把△AOB沿AB翻折,点O落在点C处,求点C的坐标.