题目内容
半径为R的圆内接正三角形的面积是
- A.
 R2
R2 - B.πR2
- C.
 R2
R2 - D.
 R2
R2
D
分析:根据题意画出图形,先求出正三角形的中心角及边心距,再根据三角形的面积公式求解即可.
解答: 解:如图所示,过O作OD⊥BC于D;
解:如图所示,过O作OD⊥BC于D;
∵此三角形是正三角形,
∴∠BOC=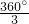 =120°.
=120°.
∵OB=OC,
∴∠BOD= ×120°=60°,
×120°=60°,
∴∠OBD=30°;
∵OB=R,
∴OD=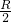 ,BD=OB•cos30°=
,BD=OB•cos30°= ,
,
∴BC=2BD=2× =
= ,
,
∴S△BOC= ×BC×OD=
×BC×OD= ×
×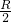 =
= ,
,
∴S△ABC=3× =
= R2.
R2.
故选D.
点评:本题考查圆的内接正三角形的性质及等边三角形的面积的计算.
规律与趋势:圆的内接正三角形的计算是圆中的基本计算,正三角形的相关性质则是解决这类问题的关键.其中,已知边长求面积,已知高求面积等都是常见的计算.
分析:根据题意画出图形,先求出正三角形的中心角及边心距,再根据三角形的面积公式求解即可.
解答:
 解:如图所示,过O作OD⊥BC于D;
解:如图所示,过O作OD⊥BC于D;∵此三角形是正三角形,
∴∠BOC=
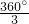 =120°.
=120°.∵OB=OC,
∴∠BOD=
 ×120°=60°,
×120°=60°,∴∠OBD=30°;
∵OB=R,
∴OD=
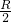 ,BD=OB•cos30°=
,BD=OB•cos30°= ,
,∴BC=2BD=2×
 =
= ,
,∴S△BOC=
 ×BC×OD=
×BC×OD= ×
×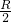 =
= ,
,∴S△ABC=3×
 =
= R2.
R2.故选D.
点评:本题考查圆的内接正三角形的性质及等边三角形的面积的计算.
规律与趋势:圆的内接正三角形的计算是圆中的基本计算,正三角形的相关性质则是解决这类问题的关键.其中,已知边长求面积,已知高求面积等都是常见的计算.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )
| A、不能构成三角形 | B、这个三角形是等腰三角形 | C、这个三角形是直角三角形 | D、这个三角形是钝角三角形 |
半径为R的圆内接正三角形的面积是( )
A、
| ||||
| B、πR2 | ||||
C、
| ||||
D、
|
以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角形,则( )
| A、这个三角形是等腰三角形 | B、这个三角形是直角三角形 | C、这个三角形是锐角三角形 | D、不能构成三角形 |