Question

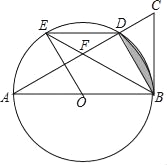
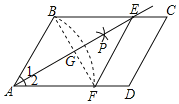
【题目】如图，以平行四边形的边分别做等边和等边．

（1）求证：；

（2）求的度数．

Answer 1

【答案】（1）见解析（2）60°

【解析】

（1）根据平行四边形的性质得出AB=CD，BC=AD，∠ABC=∠ADC，根据等边三角形的性质得出DC=DF，BC=BE，∠EBC=∠CDF=60°，求出AB=DF，BE=DA，∠ABE=∠FDA，根据SAS推出△ABE≌△FDA即可．

（2）连结EF，设∠ABC=α，则∠BCD=180°-α，通过图形上角的关系，用α表示出∠FCE，∠ABE即可得到关键条件∠ABE=∠FCE，再用同（1）的方法证明△ABE≌△FCE，得到EF=AE，进一步得到AE=AF=EF，△AEF为等边三角形求得=60°.

解：（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD，BC=AD，∠ABC=∠ADC，

∵△BCE和△CDF为等边三角形，

∴DC=DF，BC=BE，∠EBC=∠CDF=60°，

∴AB=DF，BE=DA，∠ABE=∠FDA，

在△ABE和△FDA中

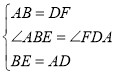
∴△ABE≌△FDA（SAS），

∴AE=AF．

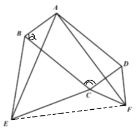
（2）连结EF，设∠ABC=α，∵四边形ABCD是平行四边形，

∴∠BCD=180°-α，

∴∠FCE=360°-∠BCE-∠DCF-∠BC,D=360°-60°-60°-(180°-α)= 60°+α，

而∠ABE=∠CBE+∠ABC=60°+α，

∴∠ABE=∠FCE，

又∵△BCE和△CDF为等边三角形，

∴EC=BE，CF=CD，

∵四边形ABCD是平行四边形，

∴AB=CD，

∴CF=AB，

在△ABE和△FCE中

,

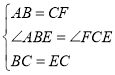∴△ABE≌△FCE(SAS),

∴EF=AE,

∴AE=AF=EF,

∴△AEF为等边三角形，

∴=60°