جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼1تاز»¸ِ³¤خھ![]() ،¢؟يخھ
،¢؟يخھ![]() µؤ³¤·½ذخ£¨ئنضذ
µؤ³¤·½ذخ£¨ئنضذ![]() £¬
£¬![]() ¾ùخھصت£¬از
¾ùخھصت£¬از![]() £©£¬رطح¼ضذذéدكسأ¼ôµ¶¾ùشب·ض³ةثؤ؟éدàح¬ذ،³¤·½ذخ£¬ب»؛َ°´ح¼2·½ت½ئ´³ةز»¸ِ´َص·½ذخ.
£©£¬رطح¼ضذذéدكسأ¼ôµ¶¾ùشب·ض³ةثؤ؟éدàح¬ذ،³¤·½ذخ£¬ب»؛َ°´ح¼2·½ت½ئ´³ةز»¸ِ´َص·½ذخ.
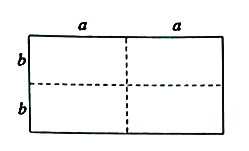
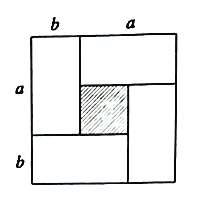
ح¼1 ح¼2
£¨1£©ح¼2ضذ´َص·½ذخµؤ±ك³¤خھ £»ذ،ص·½ذخ£¨زُس°²؟·ض£©µؤ±ك³¤خھ .£¨سأ؛¬![]() ،¢
،¢![]() µؤ´ْتت½±يت¾£©
µؤ´ْتت½±يت¾£©
£¨2£©×ذد¸¹غ²ىح¼2£¬اëؤمذ´³ِدآءذب¸ِ´ْتت½£؛![]() ثù±يت¾µؤح¼ذخأو»ض®¼نµؤدàµب¹طدµ£¬²¢ر،ب،تت؛د
ثù±يت¾µؤح¼ذخأو»ض®¼نµؤدàµب¹طدµ£¬²¢ر،ب،تت؛د![]() £¬
£¬![]() µؤتضµ¼سزشرéض¤.
µؤتضµ¼سزشرéض¤.
£¨3£©زرضھ![]() .شٍ´ْتت½
.شٍ´ْتت½![]() µؤضµخھ .
µؤضµخھ .
،¾´ً°¸،؟£¨1£©![]() £¬
£¬![]() £»£¨2£©
£»£¨2£©![]() +
+![]() £¬رéض¤¼û½âخِ£»£¨3£©
£¬رéض¤¼û½âخِ£»£¨3£©![]() .
.
،¾½âخِ،؟
£¨1£©¹غ²ىح¼ذخ¼´؟ةµأ³ِ´َص·½ذخ±ك³¤خھذ،³¤·½ذخµؤ³¤سë؟يµؤ؛ح£¬¶ّذ،ص·½ذخ±ك³¤خھذ،³¤·½ذخµؤ³¤سë؟يµؤ²î£¬¾ف´ثاَ½â¼´؟ة£»
£¨2£©¹غ²ىح¼ذخ؟ةµأ´َص·½ذخأو»![]() µبسعذ،ص·½ذخأو»
µبسعذ،ص·½ذخأو»![]() ¼سةدش³¤·½ذخأو»
¼سةدش³¤·½ذخأو»![]() £¬¾ف´ث¼´؟ةءذ³ِ´ْتت½£¬ب»؛َ½ّز»²½´ْبë؛دتتµؤت×ض¼ىرé¼´؟ة£»
£¬¾ف´ث¼´؟ةءذ³ِ´ْتت½£¬ب»؛َ½ّز»²½´ْبë؛دتتµؤت×ض¼ىرé¼´؟ة£»
£¨3£©سة£¨2£©ضذµؤ¹طدµت½½ّز»²½±نذخ¼ئثم¼´؟ة.
£¨1£©سةح¼ذخ؟ةµأ£؛´َص·½ذخµؤ±ك³¤خھ![]() £»ذ،ص·½ذخ£¨زُس°²؟·ض£©µؤ±ك³¤خھ
£»ذ،ص·½ذخ£¨زُس°²؟·ض£©µؤ±ك³¤خھ![]()
¹ت´ً°¸خھ£؛![]() £¬
£¬![]() £»
£»
£¨2£©سةح¼؟ةµأ£؛´َص·½ذخأو»![]() µبسعذ،ص·½ذخأو»
µبسعذ،ص·½ذخأو»![]() ¼سةدش³¤·½ذخأو»
¼سةدش³¤·½ذخأو»![]() £¬
£¬
¼´£؛![]() +
+![]() £»
£»
µ±![]() £¬
£¬![]() ت±£¬
ت±£¬![]() =49£¬
=49£¬![]() +
+![]() =49£¬
=49£¬
،à![]() +
+![]() ³ةء¢£»
³ةء¢£»
£¨3£©سة£¨2£©µأ£؛![]() +
+![]() £¬
£¬
،൱![]() ت±£¬
ت±£¬![]() +
+![]() £¬
£¬
¼´£؛![]() £¬
£¬
،à![]() »ٍ
»ٍ![]() £¬
£¬
،ك![]() £¬
£¬
،à![]() .
.