Question

如图，Rt△ABC中，∠ABC=90°，OA=OB=1，与x轴的正方向夹角为30°．求直线AB的解析式．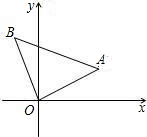

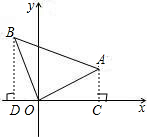Answer 1

解：作AC⊥x轴于C，BD⊥x轴D，
在Rt△AOC中，OC=1×cos30°=，AC=×1=，
∴A点坐标为（，），
OD=1×cos60°=，DB=1×sin60°=，
∴B点坐标为（-，），
设解析式为y=kx+b，
把（，），（-，）分别代入解析式得：，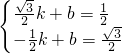
解得k=-2+，b=-1+，
∴解析式为y=（-2+）x+（-1+）．
分析：欲求直线AB的解析式，只要求出点A和点B的坐标，再根据待定系数法列方程组解答．
点评：待定系数法：先设某些未知的系数，然后根据已知条件求出未知系数的方法叫待定系数法，在求函数解析式时经常要用到．