题目内容
7.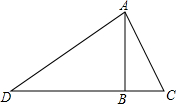 如图,点B是△ABC中DC边上一点,AC=13,AB=12,BC=5,AD=20.求BD并判断∠DAC是否是直角.
如图,点B是△ABC中DC边上一点,AC=13,AB=12,BC=5,AD=20.求BD并判断∠DAC是否是直角.
分析 先根据勾股定理的逆定理判断出△ABC的形状,再根据勾股定理求出DB的长,进而求出DC的长,那么已知△ADC的三边,根据勾股定理的逆定理即可判断∠DAC是否是直角.
解答 解:∵AC=13,AB=12,BC=5,132=122+52,
∴△ABC是直角三角形,且∠ABC=90°,
∴∠ABD=180°-∠ABC=90°,
∵AD=20,
∴BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
∴DC=DB+BC=16+5=21.
∵AD=20,AC=13,DC=21,
∴AD2+AC2=202+132=569,DC2=212=441,
∴AD2+AC2≠DC2,
∴∠DAC≠90°.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.同时考查了勾股定理.

练习册系列答案
相关题目
2.方程x2+px+q=0的两个根中,有一个且只有一个为0,则p、q应满足( )
| A. | p=0,q=0 | B. | p=0,q≠0 | C. | p≠0,q=0 | D. | p≠0,q≠0 |
 如图,四边形ABCD中:
如图,四边形ABCD中: 如图(1)(2)的截面形状是三角形,四边形.
如图(1)(2)的截面形状是三角形,四边形. 已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论.
已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论. 如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)
如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)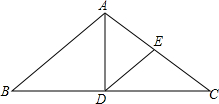 如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.
如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.