Question

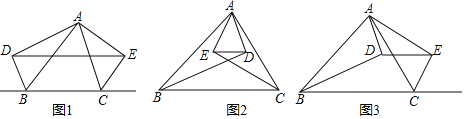
【题目】已知，△ABC，AD⊥BD于点D，AE⊥CE于点E，连接DE.

(1)如图1，若BD，CE分别为△ABC的外角平分线，求证：DE＝(AB+BC+AC).

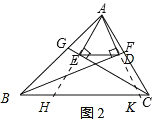
(2)如图2，若BD，CE分别为△ABC的内角平分线，(1)中的结论成立吗？若成立请说明理由；若不成立，请猜想出新的结论并证明；

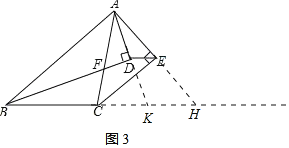
(3)如图3，若BD，CE分别为△ABC的一个内角和一个外角的平分线，AB＝8，BC＝10，AC＝7，请直接写出DE的长为______.

Answer 1

【答案】(1)证明见解析；(2)不成立.DE＝(AB+AC﹣BC)，证明见解析；(3)4.5.

【解析】

(1)根据全等三角形的判定与性质，可得AB与BK，AC与CH的关系，根据等腰三角形的性质，可得AD与DK的关系，AE与EH的关系，根据三角形中位线的性质，可得答案；(2)都是内角平分线时，可根据等腰三角形三线合一的特点来求解，由于DB平分∠ABC，且AD⊥BD，如果延长AD交BC于K，那么三角形ABK就是个等腰三角形，AD＝DK，如果延长AE到H，那么同理可证AG＝GH，AC＝CH，那么DE就是三角形AHK的中位线，DE就是HK的一半，而HK＝BK﹣BH＝BK﹣(BC﹣CH)，由于BK＝AB，CH＝AC，那么可得出DE＝(AB+AC﹣BC)；(3)证法同(1)，先根据题目给出的求法，得出GD是AC的一半，然后按(2)的方法，通过延长AF来得出DF是(BC﹣AB)的一半，由此可得出DE＝(BC+AC﹣AB)，由此即可解决问题.

(1)证明：如图1，分别延长AE、AD交BC于H、K，

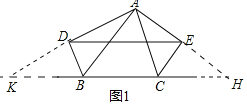
在△BAD和△BKD中，

∵，

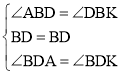∴△BAD≌△BKD(ASA)，

∴AD＝KD，AB＝KB，

同理可证，AE＝HE，AC＝HC，

∴DE＝HK，

又∵HK＝BK+BC+CH＝AB+BC+AC，

∴DE＝(AB+AC+BC)；

(2)解：结论不成立.DE＝(AB+AC﹣BC).

理由：如图2，分别延长AE、AD交BC于H、K，

在△BAD和△BKD中，

∵，

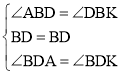∴△BAD≌△BKD(ASA)，

∴AD＝KD，AB＝KB，

同理可证，AE＝HE，AC＝HC，

∴DE＝HK，

又∵HK＝BK﹣BH＝AB+AC﹣BC，

∴DE＝(AB+AC﹣BC).

(3)解：分别延长AE、AD交BC或延长线于H、K，

在△BAD和△BKD中，

∵，

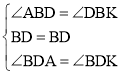∴△BAD≌△BKD(ASA)，

∴AD＝KD，AB＝KB

同理可证，AE＝HE，AC＝HC，

∴DE＝KH

又∵KH＝BC﹣BK+HC＝BC+AC﹣AB.

∴DE＝(BC+AC﹣AB)，

∵AB＝8，BC＝10，AC＝7，

∴DE＝(10+7﹣8)＝4.5，

故答案为4.5.