题目内容
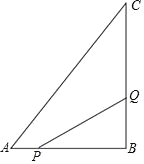
【题目】在△ABC中，AB=10cm，BC=16cm，∠B=90°，点P从点A开始沿着AB边向点B以1cm/s的速度移动（到B停止），点Q从点B开始沿着BC边向点C以2cm/s的速度移动（到C停止）．如果P、Q分别从A、B同时出发，经过几秒钟，使△PBQ的面积是△ABC面积的
？
【答案】经过4秒或6秒，△PBQ的面积是△ABC面积的
．
【解析】
设经过x秒钟，△PBQ的面积是△ABC面积的，分0＜x≤8及8＜x≤10两种情况，根据三角形的面积公式找出关于x的一元二次方程（或一元一次方程），解之即可得出结论．
设经过 x 秒钟，△PBQ 的面积是△ABC 面积的， 当 0＜x≤8 时，根据题意得：
×2x（10﹣x）=×10×16×， 整理得：x2﹣10x+24=0，
解得：x1=4，x2=6；
当 8＜x≤10 时，
×16（ 10﹣x）=×10×16× 
，整理得：16x=112，
解得：x=7（舍去）．
答：经过4秒或6秒，△PBQ 的面积是△ABC面积的．
练习册系列答案
相关题目
