题目内容
(本题满分7分)如图一张边长为20cm 的正方形硬纸板,把它的四个角都剪去一个边长为acm的小正方形,然后把它折
成一个无盖的长方体,请回答下列问题:
(1)请用含有a的代数式表示无盖长方体的体积V;(正确列出式子即可,不必化简)
(2)如果剪去的小正方形边长按整数值依次变化,即分别取1cm,2cm,3cm, ,10cm时,折成的无盖长方体盒子的容积分别是多少?请完成下表:
a(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
V(cm3) | 324 | 512 | 500 | 384 | 252 | 128 | 36 | 0 |
(3)根据表格回答,当a取什么正整数时,容积V的值最大?

(1) 2分(2)588,576 6分(3)
2分(2)588,576 6分(3) 时 7分
时 7分
【解析】
试题分析:(1)用a表示出底面正方形的边长,然后根据体积公式解答即可;
(2)根据(1)中得出的关系式,代入数据x=3、4进行计算即可得到对应的V的值;
(3)根据表格数据的变化规律即可得解;
试题解析:(1)根据题意,无盖的长方体的底面正方形的边长为20-2a,高为a,∴V=a(20-2a)2;
(2)在V=a(20-2a)2中,
当a=3时,V=3×(20-2×3)2=3×196=588,
当a=4时,V=4×(20-2×4)2=4×144=576,
(3)观察上表,可以发现容积V的值不是随着x的值的增大而增大的,
从表中可知,当a取整数3时,容积V最大;
考点:1.列代数式;2.求代数式的值.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.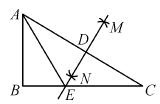


 D.-
D.-

 ,其中a=-1,b=
,其中a=-1,b= .
.

 的值为0,则代数式
的值为0,则代数式 的值为 ( )
的值为 ( )