��Ŀ����
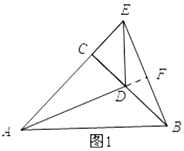
����Ŀ����ͼ1������������������![]() ��
��![]() ƴ����һ������
ƴ����һ������![]() ��
��![]() ��
��![]() .
.
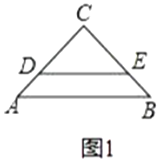
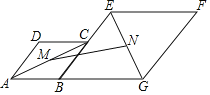
��1����������
��ͼ2���̶�![]() ����
����![]() ���Ŷ���
���Ŷ���![]() ��ת��ʹ��
��ת��ʹ��![]() ����
����![]() ����.
����.
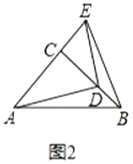
��գ��߶�![]() ��
��![]() �Ĺ�ϵ�Ǣ�λ�ù�ϵ��______����������ϵ��______
�Ĺ�ϵ�Ǣ�λ�ù�ϵ��______����������ϵ��______
��2����ʽ̽��
��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ3��λ��ʱ����1���еĽ��ۻ���������˵�����ɣ�
��ת��ͼ3��λ��ʱ����1���еĽ��ۻ���������˵�����ɣ�
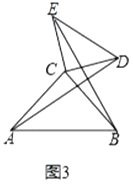
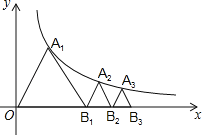
��3���������
��ͼ4����֪�߶�![]() ���߶�
���߶�![]() ����
����![]() Ϊ����һ��������
Ϊ����һ��������![]() ������
������![]() �����ű�
�����ű�![]() �ı仯���߶�
�ı仯���߶�![]() �ij�Ҳ�ᷢ���仯.��ֱ��д���߶�
�ij�Ҳ�ᷢ���仯.��ֱ��д���߶�![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
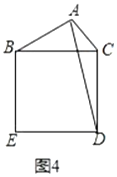
���𰸡���1����![]() ����
����![]() ����2�������������3��
����2�������������3��![]()
��������
��1���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() .����
.����![]() ֤��
֤��![]() ����ȫ�������ε����ʿɵõ�
����ȫ�������ε����ʿɵõ�![]() ��Ȼ������
��Ȼ������![]() ��
��![]() ���ɵõ�
���ɵõ�![]() ��
��
��2����ͼ2��ʾ����![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
��![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() .��֤��
.��֤��![]() ��Ȼ������
��Ȼ������![]() ֤��
֤��![]() ����ȫ�������ε����ʿɵõ�
����ȫ�������ε����ʿɵõ�![]() ��Ȼ����
��Ȼ����![]() ��
��![]() ����֤��
����֤��![]() ��
��
��3������![]() ��
��![]() ��ȡ
��ȡ![]() ������
������![]() �����ڵ���ֱ��
�����ڵ���ֱ��![]() �����
�����![]() �ij���Ȼ�����������ε����߹�ϵ�����
�ij���Ȼ�����������ε����߹�ϵ�����![]() ��ȡֵ��Χ���������
��ȡֵ��Χ���������![]() ֤��
֤��![]() ����ȫ�������ε����ʵõ�
����ȫ�������ε����ʵõ�![]() ���ʴ˿����
���ʴ˿����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�⣺��1���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
��![]() ��
��![]() ��
��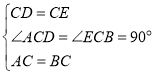 ��
��
��![]() .
.
��![]() ��
��![]() .
.
�֡�![]() ��
��
��![]() .
.
��![]() .
.
�ʴ�Ϊ��![]() ��
��![]() .
.
��2����ͼ2��ʾ����![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
��![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() .
.
��![]() ��
��
��![]() ����
����![]() .
.
��![]() ��
��![]() ��
�� ��
��
��![]() .
.
��![]() ��
��![]() .
.
�֡�![]() ��
��
��![]() .
.
��![]() .
.
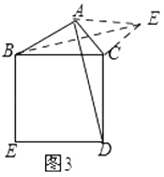
��3����ͼ3��ʾ������![]() ��
��![]() ��ȡ
��ȡ![]() ������
������![]() .
.
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
��
��![]() ����
����![]() .
.
��![]() ��
��![]() ��
��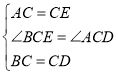 ��
��
��![]() .
.
��![]() .
.
��![]() .
.

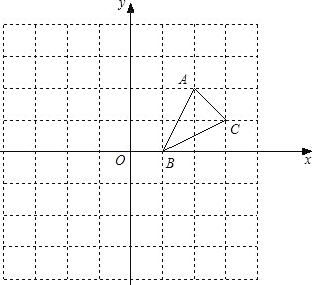
 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�